AD9776A/AD9778A/AD9779A
Rev. B | Page 37 of 56
INTERPOLATION FILTER BANDWIDTH LIMITS
The AD9776A/AD9778A/AD9779A use a novel interpolation
filter architecture that allows DAC IF frequencies to be gener-
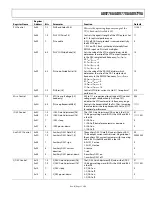
ated anywhere in the spectrum. Figure 68 shows the traditional
choice of DAC IF output bandwidth placement. Note that there
are no possible filter modes in which the carrier can be placed
near 0.5 × f
DATA
, 1.5 × f
DATA
, 2.5 × f
DATA
, and so on.
10
–80
–4
4
f
OUT
(× Input Data Rate),
ASSUMING 8× INTERPOLATION
AT
T
E
NUAT
IO
N
(
d
B)
0
–10
–20
–30
–40
–50
–60
–70
–3
–2
–1
0
1
2
3
+
f
DAC
/2
+
f
DAC
/4
+
f
DAC
/8
B
A
SEB
A
N
D
–
f
DA
C
/8
–
f
DA
C
/4
–
f
DA
C
/2
06
45
2-
0
65
Figure 68. Traditional Bandwidth Options for TxDAC Output IF
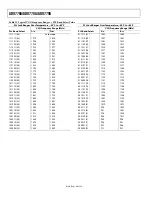
The filter architecture not only allows the interpolation filter
pass bands to be centered in the middle of the input Nyquist
zones (as explained in this section), but also allows the possi-
bility of a 3 × f
DAC
/8 modulation mode when interpolating by 8.
With all of these filter combinations, a carrier of given bandwidth
can be placed anywhere in the spectrum and fall into a possible
pass band of the interpolation filters. The possible bandwidths
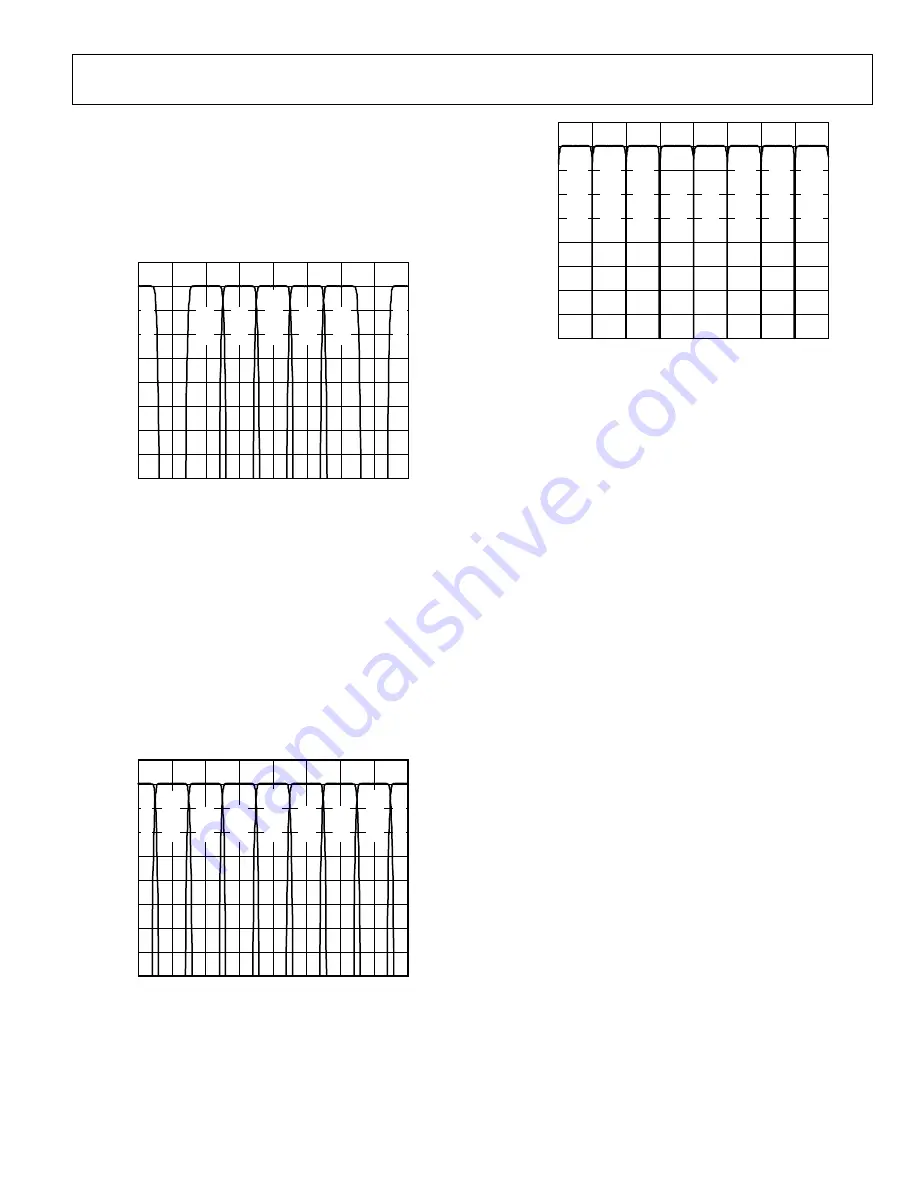
accessible with the filter architecture are shown in Figure 69 and
Figure 70. Note that the shifted and nonshifted filter modes are
all accessible by programming the filter mode for a particular
interpolation rate.
10
–80
–4
4
f
OUT
(× Input Data Rate),
ASSUMING 8× INTERPOLATION
AT
T
E
NUAT
IO
N
(
d
B)
0
–10
–20
–30
–40
–50
–60
–70
–3
–2
–1
0
1
2
3
–
f
DA
C
/2
–3 ×
f
DAC
/8
–
f
DA
C
/4
–
f
DA
C
/8
B
A
SEB
A
N
D
+
f
DAC
/8
+
f
DAC
/4
+3
×
f
DA
C
/8
+
f
DAC
/2
06
45
2-
0
66
Figure 69. Nonshifted Bandwidths Accessible with the Filter Architecture
10
–80
–4
4
f
OUT
(× Input Data Rate),
ASSUMING 8× INTERPOLATION
AT
T
E
N
U
AT
IO
N
(
d
B
)
0
–10
–20
–30
–40
–50
–60
–70
–3
–2
–1
0
1
2
3
S
H
IF
T
E
D
– 3 ×
f
DAC
/8
SH
IF
T
ED
–
f
DA
C
/4
SH
IF
T
ED
–
f
DA
C
/8
SH
IF
T
ED
–
D
C
SH
IF
T
ED
+
D
C
SH
IF
T
ED
+
f
DA
C
/8
SH
IF
T
ED
+
f
DA
C
/4
SH
IF
T
ED
+
3
×
f
DA
C
/8
06
45
2-
08
7
Figure 70. Shifted Bandwidths Accessible with the Filter Architecture
With this filter architecture, a signal placed anywhere in the
spectrum is possible. However, the signal bandwidth is limited
by the input sample rate of the DAC and the specific placement
of the carrier in the spectrum. The bandwidth restriction resulting
from the combination of filter response and input sample rate is
often referred to as the synthesis bandwidth, because this is the
largest bandwidth that the DAC can synthesize.
The maximum bandwidth condition exists if the carrier is
placed directly in the center of one of the filter pass bands. In
this case, the total 0.1 dB bandwidth of the interpolation filters
is equal to 0.8 × f
DATA
. As Table 19 shows, the synthesis band-
width as a fraction of the DAC output sample rate drops by a
factor of 2 for every doubling of interpolation rate. The mini-
mum bandwidth condition exists, for example, if a carrier is
placed at 0.25 × f
DATA
. In this situation, if the nonshifted filter
response is enabled, the high end of the filter response cuts off
at 0.4 × f
DATA
, thus limiting the high end of the signal bandwidth.
If the shifted filter response is instead enabled, then the low end
of the filter response cuts off at 0.1 × f
DATA
, thus limiting the low
end of the signal bandwidth. The minimum bandwidth speci-
fication that applies for a carrier at 0.25 × f
DATA
is therefore 0.3 ×
f
DATA
. The minimum bandwidth behavior is repeated over the
spectrum for carriers placed at (±n ± 0.25) × f
DATA
, where n is
any integer.
Digital Modulation
The digital quadrature modulation occurs within the interpolation
filter. The modulation shifts the frequency spectrum of the
incoming data by the frequency offset selected. The frequency
offsets available are multiples of the input data rate. The
modulation is equivalent to multiplying the quadrature input
signal by a complex carrier signal, C(t), of the following form:
C
(
t
) = cos(
ω
c
t
) +
j
sin(
ω
c
t
)