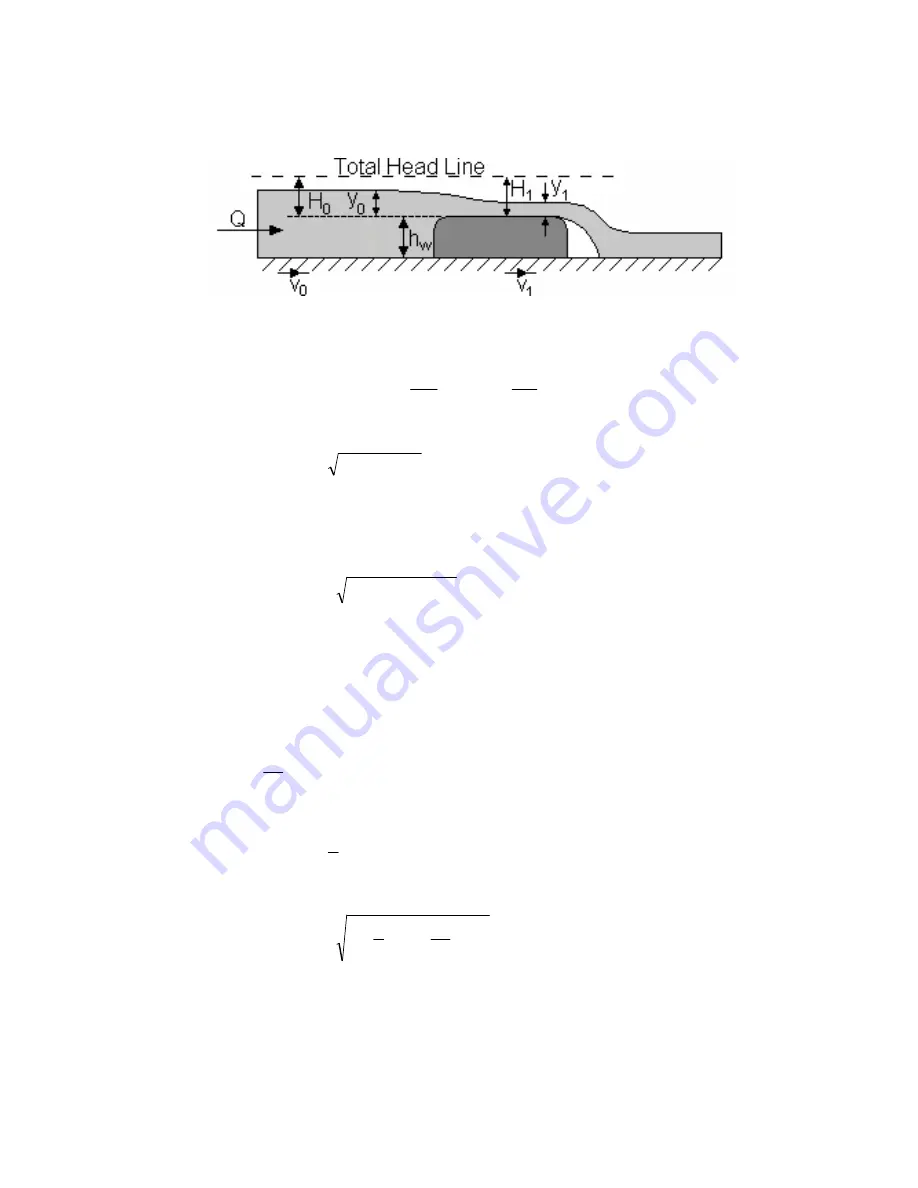
37
Theory
From conservation of energy and ignoring losses:
H
0
= H
1
= y
0
+
g
2
v
2
0
= y
1
+
g
2
v
2
1
Therefore
v
1
=
(
)
1
0
y
H
g
2
−
The flow rate Q is given by:
Q
= y
1
v
1
b
1
= b
(
)
3
1
2
1
0
y
y
H
g
2
−
Provided that the weir is not submerged (downstream water level is low), the flow over a
Broad Crested Weir may be assumed to be critical as it passes over the weir. Hence
H
0
y
1
2
– y
1
³
= maximum
At maximum
dh
dq
= 0
= 2 H
0
y
1
– 3y
1
²
Therefore
y
1
=
3
2
H
0
Therefore
Q
max
= b
−
3
0
3
0
H
27
8
H
9
4
g
2
= 1.705 bH
0
3/2
The actual flow over a Broad Crested weir will be less than the theoretical flow so a
coefficient is introduced into the equation:

































