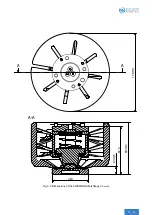
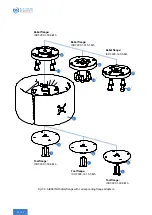
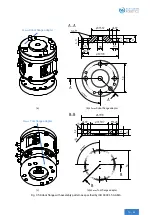
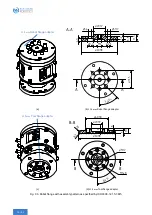
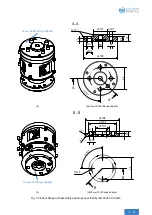
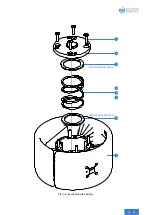
In the case of a deviating center of gravity position
l
s
, the additional or reduced force that is required to cause
actuation can be calculated by using the following formula:
F
xy
±
=
0
.
6
·
m
g
·
(
l
s
−
0
.
2
)
l
z
+
0
.
0364
(5.2)
m
g
is the payload, consisting of the weight of the gripper
m
G
and load
m
L
in [
kg
]. In order to calculate the maxi-
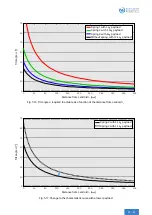
mum actuation force, one can (depending on the pressure spring configuration) refer to the maximum permissible
payloads (
2
.
5 kg
,
5 kg
,
7
.
5 kg
,
10 kg
).
l
s
defines the new distance from centroid in [
m
] while
l
z
defines the lever arm
in [
m
] at which the actuation force
F
xy
takes effect.
If the center of gravity is lower (
l
s
>
200 mm
), for example at
l
s
=
300 mm
, a payload of
10 kg
(without spring) and a
lever arm of
l
z
=
50 mm
would require an additional actuation force
F
xy
+
of approx.
6
.
9 N
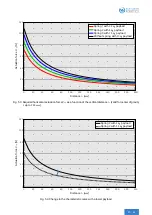
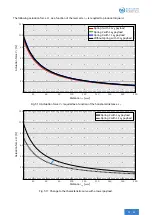
. From the characteristic
curves in
one can read off an actuation force of
46 N
when
l
z
=
50 mm
with a payload of
10 kg
(without
spring). As a result of shifting the center of gravity to
l
s
=
300 mm
, the calculated force
F
xy
+
=
6
.
9 N
can be added
to the actuation force from the diagram (
F
xy
=
46 N
), thereby producing an actuation force of
52
.
9 N
.
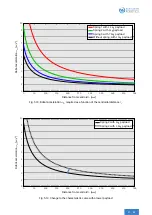
If the center of gravity position is higher (
l
s
<
200 mm
), for example at
l
s
=
60 mm
, a payload of
10 kg
(without
spring) and a lever arm of
l
z
=
50 mm
would produce a reduction in the actuation force
F
xy
−
of approx.
−
9
.
7 N
.
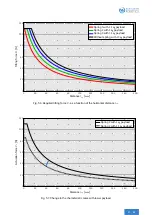
This means that the actuation force
F
xy
=
46 N
from
would fall to
36
.
3 N
.