21
The effective noise for a galaxy in the absence of source continuum is computed
using:
€
Noise
2
=
N
exp
Ω
eff
σ
eff
2
P
2
,
where
€
σ
eff
2
is the effective noise variance per pixel per exposure; Ω
eff
is the effective solid
angle of the source; and
P
is the pixel scale. The effective noise has several contributions, as
described in §7.F.
The effective solid angle for computing S/N ratios for the background-‐limited case
(relevant here) depends on the normalized probability distribution Π(
x
) for the apparent
2D angular positions
x
[rad] of line photons arriving from a galaxy. It is given by
€
Ω
eff
=
1
[
Π
(
x
)]
2
d
2
x
∫
=
1
˜
Π
(
u
)
2
d
2
u
∫
,
where in the second equality we have considered the Fourier transform
€
˜
Π
(
u
)
, which
depends on the spatial frequency vector
u
. Note that we define the Fourier transform using
spatial frequencies,
€
Π
(
x
)
=
˜
Π
(
u
)
e
2
π
i
u
⋅
x
d
2
u
∫
⇔
˜
Π
(
u
)
=
Π
(
x
)
e
−
2
π
i
u
⋅
x
d
2
x
∫
.
€
˜
Π
(
u
)
is given by the product of the Fourier transform of the normalized galaxy profile
€
˜
f
(
u
)
and the Fourier transform of the PSF
€
˜
G
(
u
)
. “Normalization” here means that
€
˜
f
(
0
)
=
˜
G
(
0
)
=
˜
Π
(
0
)
=
1
. Also, we can see that for a top-‐hat distribution where the probability
density is equal to Ω
−1
(within some region of angle Ω) and 0 (elsewhere), the effective area
is Ω
eff
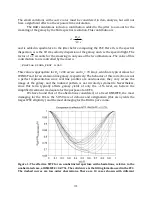
=Ω, hence its name. Smaller solid angle objects (i.e. smaller galaxies or smaller PSFs)
will have lower noise and hence we can expect to reach lower flux sensitivities in these
cases.
In BAO mode, we restrict the integral over
u
to the first Brillouin zone (|
u
x
|, |
u
y
| <
0.5/
P
), which provides the correct expected detection SNR for a large number of
undersampled images naively sinc-‐interpolated onto a common grid and coadded. For
practical WFIRST cases this restriction has little effect on the galaxy yields.
The expected SNR (“SNRe”) is obtained as the ratio of the signal (calculated using
the
true
line flux) to the noise. For the BAO, the default option is to impose cuts on the
observed SNR (“SNRo”), which is the measured signal divided by the noise. The two are not
identical (SNRe is a property of the galaxy and the instrument, whereas SNRo is a random
variable); see §7.E.
The statistical uncertainty (not including aliasing effects) in the centroid in the
x
1
-‐
direction is
€
σ
x
−
2
=
I
C
[source counts]
[background counts per unit solid angle]
,