19
12
Definite Integrals
(Trapezoidal rule)
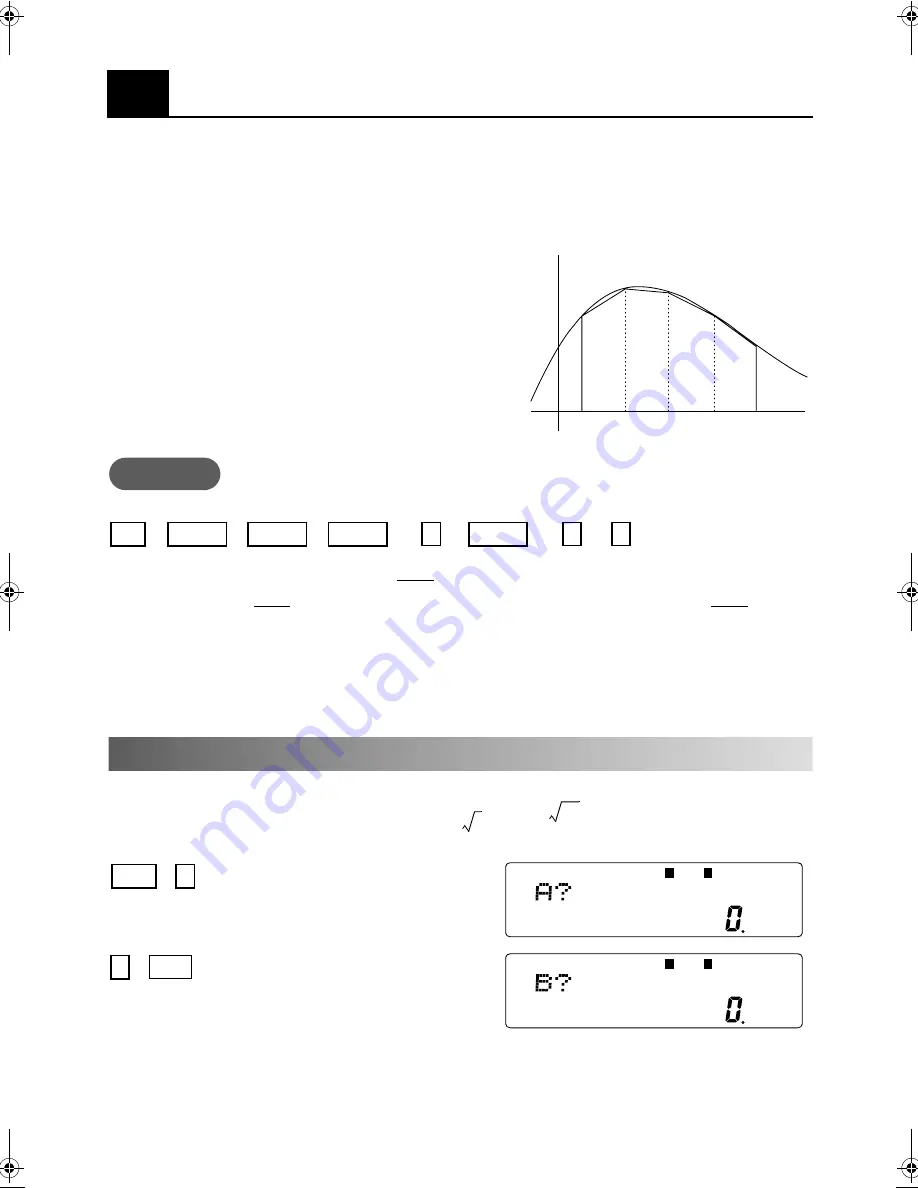
Approximations of the value of definite integrals may be obtained as follows:
:number of trapezoids
For larger the approximation improves, and as
tends to infinity it agrees with the precise value of
the definite integral.
Program
?→ A:?→ B:?→ C:1→ D:
(√ A)÷2→ Y:Lbl 1:
(A(C - D)+ DB)
÷ C → X:Y +(√ X)→ Y:D +1→ D:D ≠ C ⇒ Goto 1:Y +(√ B)÷2→
Y:
(B - A)Y ÷ C → Y:Y <
89 STEP
>
INPUT
A
,
B
: interval of integration [
A
,
B
]
C
: number of trapezoids
OUTPUT
Y
: value of the definite integral
Execution Example:
Calculate the value of the definite integral
.
x
( )
x
d
A
B
∫
h
2
---
f A
( )
2
f A h
+
(
)
2
f A
2
h
+
(
) …
2
f B h
–
(
)
f B
( )
+
+
+
+
+
(
)
≈
h
B A
–
n
-------------
=
n
b
a
n
n
ON
MODE
MODE
MODE
1
PRGM
MODE
1
COMP
1
P1
x x
d
0
10
∫
10
20
3
--------------
21.08185107
=
=
Prog
1
S A
D R
P1
P1 P2 P3 P4
G
0
EXE
S A
D R
P1
P1 P2 P3 P4
G
関数電卓事例集
.book
1
9
ページ
2002年9月2日 月曜日 午後6時51分
Summary of Contents for 3950P
Page 1: ......
Page 46: ...MEMO MEMO MEMO MEMO...
Page 47: ...Authors Dr Yuichi Takeda Research and Development Initiative Chuo University...
Page 48: ......