298
u
u
u
u
u
2-Prop
Z
Interval
2-Prop
Z
Interval
calculates the confidence interval when the proportions of two
samples are known. The 2-Prop
Z
Interval is applied to standard normal distribu-
tion.
The following is the confidence interval.
Left
=
– –
Z
)
2
x
1
n
1
x
2
n
2
n
1
n
1
x
1
1–
n
1
x
1
+
n
2
n
2
x
2
1–
n
2
x
2
Right
=
– +
Z
)
2
x
1
n
1
x
2
n
2
n
1
n
1
x
1
1–
n
1
x
1
+
n
2
n
2
x
2
1–
n
2
x
2
n
1
,
n
2
: sample size
x
1
,
x
2
: data
Perform the following key operation from the statistical data list.
4
(INTR)
1
(Z)
4
(2-P)
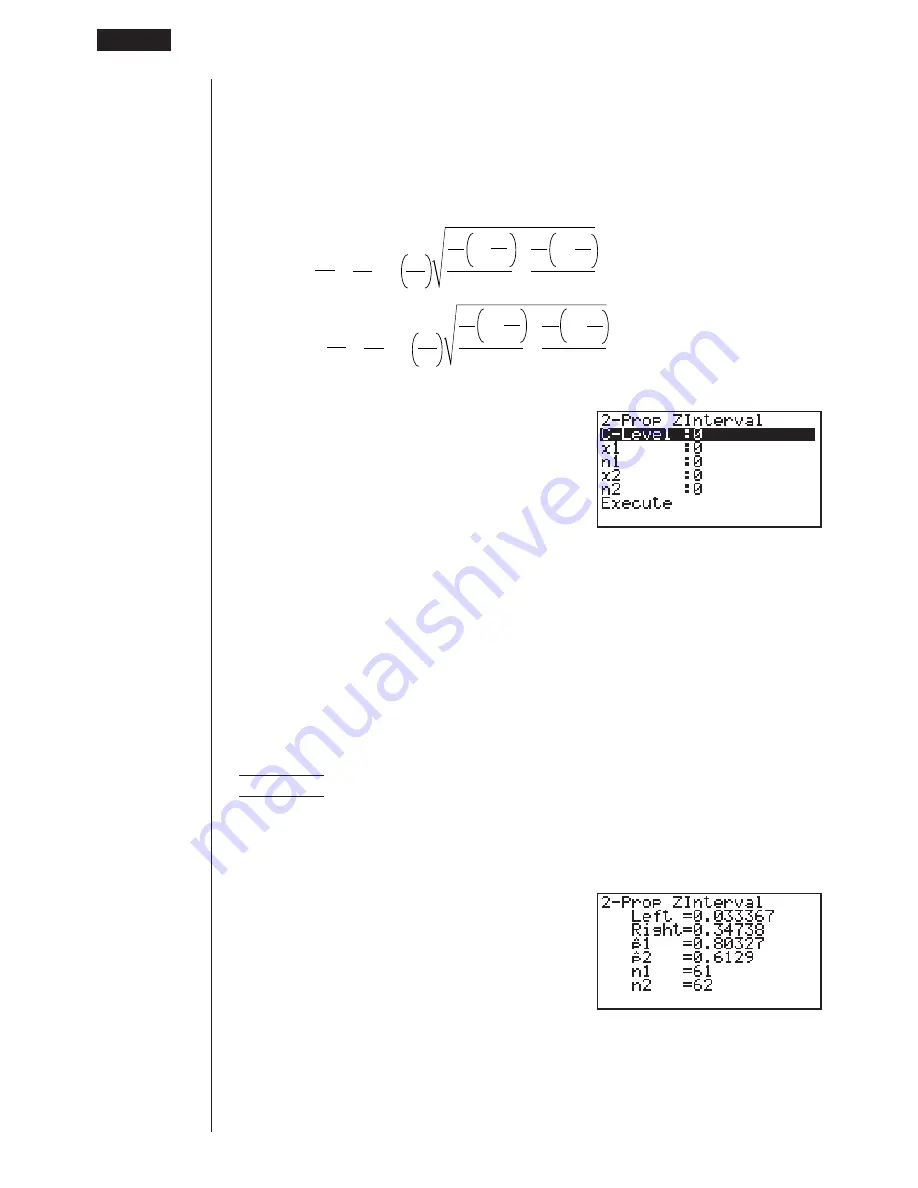
Data is specified using parameter specification. The following shows the meaning
of each item.
C-Level ........... confidence level (0
<
C-Level < 1)
x
1
.................... sample 1 data value (
x
1
>
0)
n
1
.................... sample 1 size (positive integer)
x
2
.................... sample 2 data value (
x
2
>
0)
n
2
.................... sample 2 size (positive integer)
Execute .......... Executes a calculation
Example
To calculate the 2-Prop
Z
Interval using parameter value
specification
For this example, we will obtain the 2-Prop
Z
Interval when
C-Level = 0.95,
x
1
= 49,
n
1
= 61,
x
2
= 38 and
n
2
= 62.
a.jf
w
ej
w
gb
w
di
w
gc
w
1
(CALC)
Left ................. interval lower limit (left edge)
Right ............... interval upper limit (right edge)
18 - 7
Confidence Interval
Summary of Contents for CFX-9970G
Page 22: ... CFX 9970G ...
Page 452: ...435 1 2 3 4 5 Program for Circle and Tangents No 4 Step Key Operation Display ...
Page 453: ...436 Program for Circle and Tangents No 4 Step Key Operation Display 6 7 8 9 10 ...
Page 454: ...437 11 12 13 14 15 Program for Circle and Tangents No 4 Step Key Operation Display ...
Page 455: ...438 16 17 18 Program for Circle and Tangents No 4 Step Key Operation Display ...
Page 458: ...441 1 2 3 4 5 Program for Rotating a Figure No 5 Step Key Operation Display ...















































