20021201
6-3 Recursive and Explicit Form of a Sequence
ClassPad supports use of three types of sequence expressions:
a
n
+
1
=,
a
n
+
2
=
and
a
n
E
.
Generating a Number Table
In addition to ordered pair tables, the Sequence application provides you with the means to
generate arithmetic sequence tables
*
1
, geometric sequence tables
*
2
, progression of
difference tables
*
3
, and Fibonacci sequence tables
*
4
.
*
1
sequence table for determining if sequence is an arithmetic sequence
*
2
sequence table for determining if sequence is a geometric sequence
*
3
sequence table for determining if sequence is a progression of difference
*
4
sequence table for determining if sequence is a Fibonacci sequence
Example:
To create a table (Fibonacci sequence table) for the recursion
a
n
+
2
=
a
n
+
1
+
a
n
,
a
1
= 1,
a
2
= 1
u
ClassPad Operation
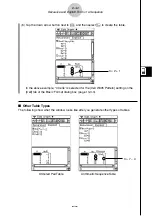
(1) Start up the Sequence Editor.
• If you have another application running, tap
m
and then
H
.
• If you have the Sequence application running, tap
O
and then [Sequence Editor].
(2) Tap the [Recursive] tab.
(3) Specify the recursion type by tapping [Type] and then [
a
n
+
2
Type
a
1
,
a
2
].
(4) Input the recursion expression.
• Tap the input box to the right of
a
n
+
2
:, and then use the procedures under “6-2
Inputting an Expression in the Sequence Application” to input the following.
[
n
,
a
n
] [
a
n
+
1
]
+
[
n
,
a
n
] [
a
n
]
E
(5) Input the initial value.
1E1E
(6) Tap
8
.
• This causes the Sequence Table Input dialog box to appear.
(7) Input the
n
-value range as shown below, and then tap [OK].
Start:1
End:5
6-3-1
Recursive and Explicit Form of a Sequence
20030201