SR260B_SR-281N_Dutch_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/3/31
-D27-
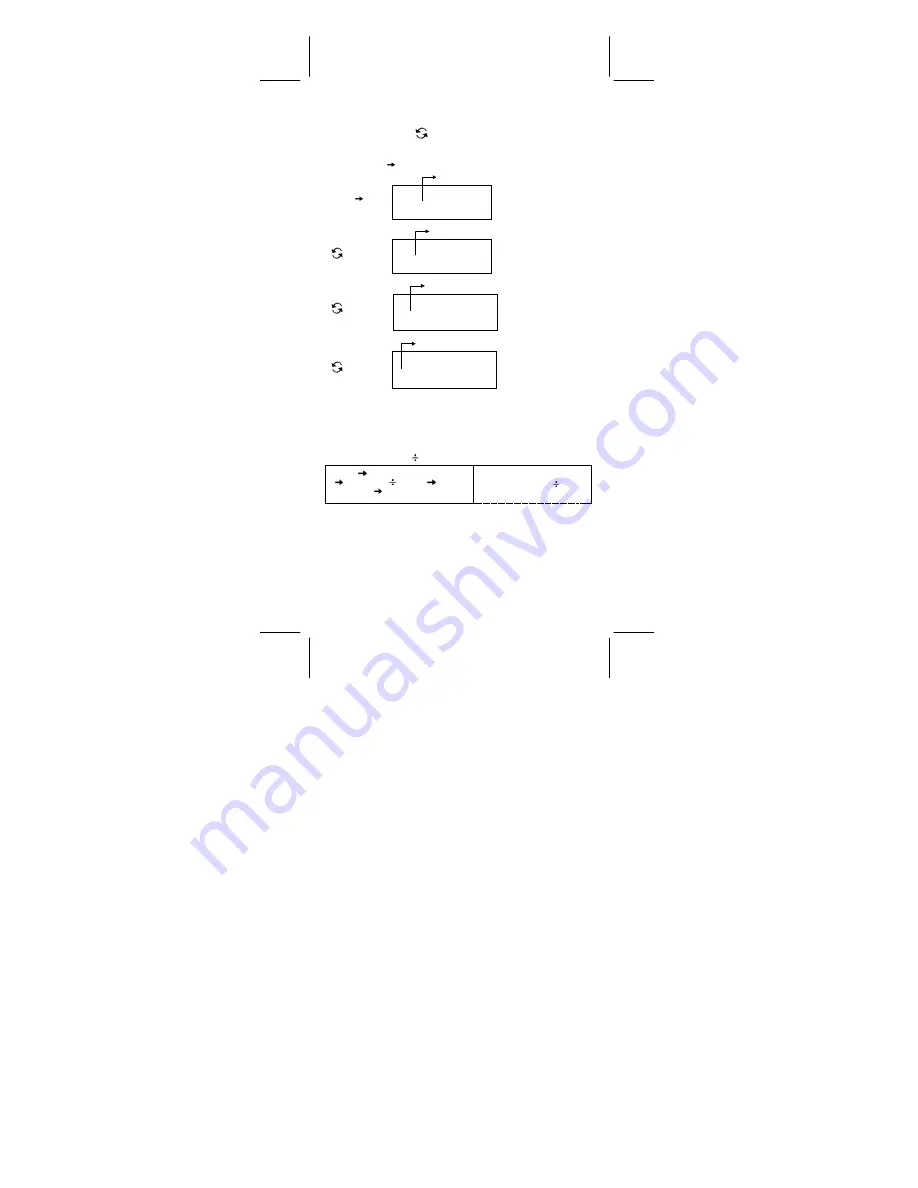
In de binaire getalbasis wordt onmiddellijk na de berekening, blok 1
weergegeven. De andere blokken ( blok 2 ~ blok 4 ) worden
weergegeven door op [
] te drukken.
Voer bijvoorbeeld 47577557
16
in.
Druk op [ 2nd ] [ HEX ] 47577557
[ 2nd ] [ BIN ]
0 1 0 1 0 1 1 1
b
DEG BIN
– –
Toont aan dat Blok 1 momenteel weergeven wordt
[
]
0 1 1 1 0 1 0 1
b
DEG BIN
–
–
Toont aan dat Blok 2 momenteel weergeven wordt
[
]
0 1 0 1 0 1 1 1
b
DEG BIN
– –
Toont aan dat Blok 3 momenteel weergeven wordt
[
]
0 1 0 0 0 1 1 1
b
DEG BIN
– – –
Toont aan dat Blok 4 momenteel weergeven wordt
47577557
16
= Blok 4 + Blok 3 + Blok 2 + Blok 1
= 01000111010101110111010101010111
2
Rekenkundige basisbewerkingen in andere
getalbasissen
¾
1IEIF
16
+ 1234
10
1001
2
= 1170
8
DEG
OCT
h 1 IE IF + 1 2 3 4
b 1
[ 2nd ] [ HEX ] 1E F [ + ] [ 2nd ]
[ DEC ] 1234 [ ] [ 2nd ] [ BIN ] 1001
[ = ] [ 2nd ] [ OCT ]
0 0 0 0 0 0 0 1 1 7 0
o
Negatieve uitdrukkingen
In de binaire, octale, en hexadecimale getalbasissen, stelt de
rekenmachine negatieve nummers voor aan de hand van de
complementnotatie. Het complement is het resultaat dat bekomen
wordt in deze getalbasis door het getal van
100000000000000000000000000000000 af te trekken, door op de
[ NEG ] toets in een niet-decimale getalbasis te drukken.














































