EE Pro for TI-89, 92 Plus
Equations - AC Circuits
56
23.3 Impedance
↔
Admittance
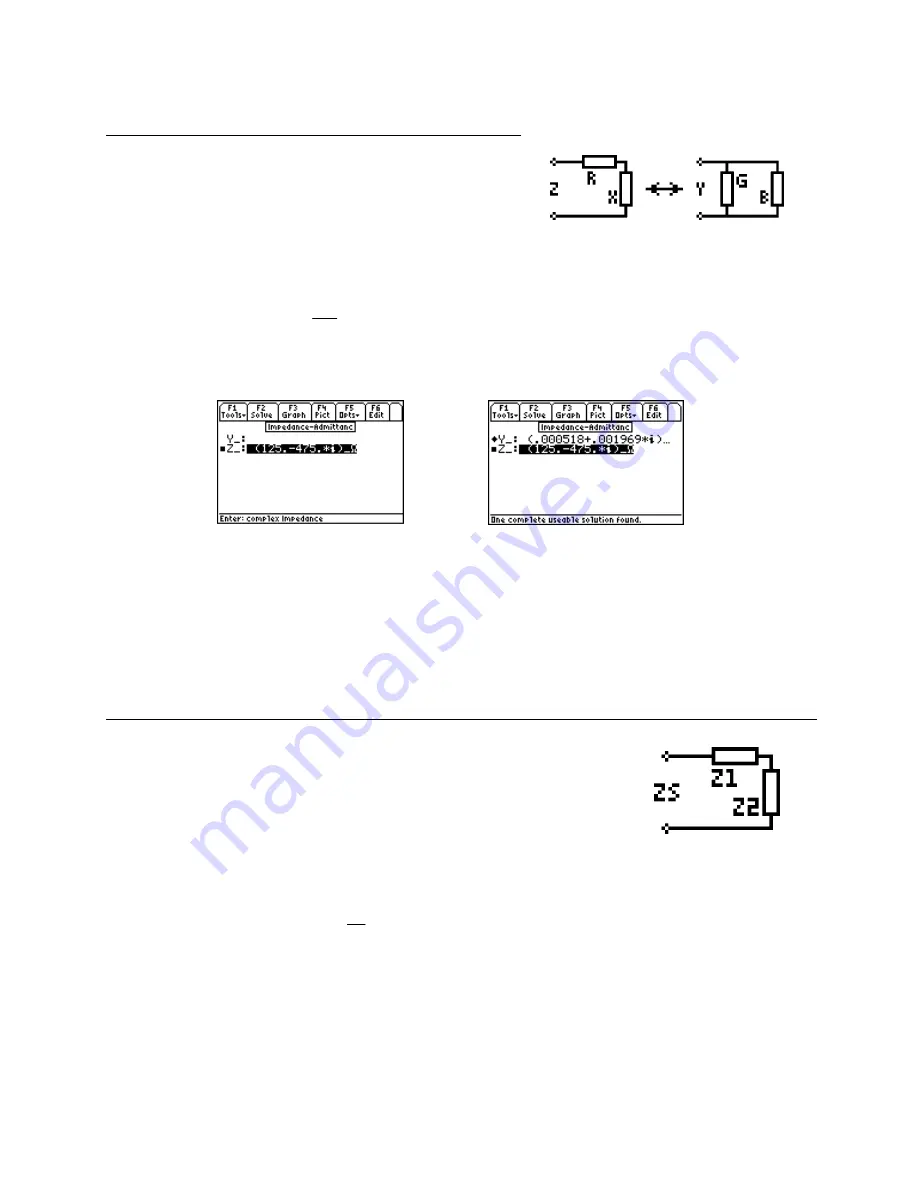
The equation is designed to convert impedances to admittances
with unit management built-in. As shown in the figure to the right,
an impedance Z consists of a real and reactive components (R and
X) to describe it. The admittance Y consists of real and reactive
components (G and B) to describe it. The variables Z and Y have
an _ attached to them to add emphasize that they
are complex in general and have units attached.
Y
Z
_
_
=
1
Eq. 23.3.1
Example 23.3 -
Find the admittance of an impedance consisting of a resistive part of 125
Ω
and a reactance part
of 475_
Ω
.
Entered Value
Calculated Result
Solution -
Press
„
to display the input screen, enter all the known variables and press
„
to solve the
equation. The computed results are shown in the screen displays above.
-PQYP8CTKCDNGU<
K
A
Ω
%QORWVGF4GUWNVU;
K
A5KGOGPU
23.4 Two Impedances in Series
These equations combine two impedances Z1 and Z2 in series with real and imaginary
parts RR1 and XX1, RR2 and XX2, respectively. The impedances Z1 and Z2 are
expressed by their magnitudes Z1m and Z2m, and phase angles
θ
1 and
θ
2
respectively. The combined result of the two impedances in series is an impedance with
a magnitude Zm and a phase angle
θ
.
abs Zm
R
X
b g
2
2
2
=
+
Eq. 23.4.1
θ =
F
HG
I
KJ
−
tan
1
X
R
Eq. 23.4.2
R
RR
RR
=
+
1
2
Eq. 23.4.3
X
XX
XX
=
+
1
2
Eq. 23.4.4
abs Z m
RR
XX
1
1
1
2
2
2
b
g
=
+
Eq. 23.4.5
abs Z m
RR
XX
2
2
2
2
2
2
b
g
=
+
Eq. 23.4.6
















































