MATRIX 400™ QUICK GUIDE
15
OPTICAL ACCESSORY SELECTION
Refering to Figure 18 and the formula below, use the data in the following table to calculate the FOV for your
application.
Model Lens
Viewing Angle
Horizontal
Viewing
Angle
Vertical
Viewing
Angle
Diagonal
Min Focus Distance
mm
Lighting System
LNS-1109 9mm
48.5°
39.5°
60°
85
LT-002
LNS-1112 12.5mm
37°
30°
46.5°
85
LT-002
LNS-1116 16mm
28.5°
23°
36°
85
LT-001
LNS-1125 25mm
18.5°
15°
23.5°
135
LT-001
LNS-1135 35mm
13°
10,5°
16.5°
235
LT-006
400-400-0x0
(SXGA)
LNS-1150 50mm
9°
7°
11.5°
500
LT-006
LNS-1006 6mm
59.5°
46.5°
71°
85
LT-002
LNS-1109 9mm
40.5°
31°
49.5°
85
LT-002
LNS-1112 12,5mm
31°
23.5°
38°
85
LT-002
LNS-1116 16mm
24°
18°
30°
85
LT-001
LNS-1125 25mm
15°
11.5°
19°
135
LT-001
LNS-1135 35mm
11°
8.5°
13.5°
235
LT-006
400-600-0x0
(UXGA)
LNS-1150 50mm
7.5°
5.5°
9.5°
500
LT-006
The viewing angle has a tolerance of
±
1° depending on the focus distance.
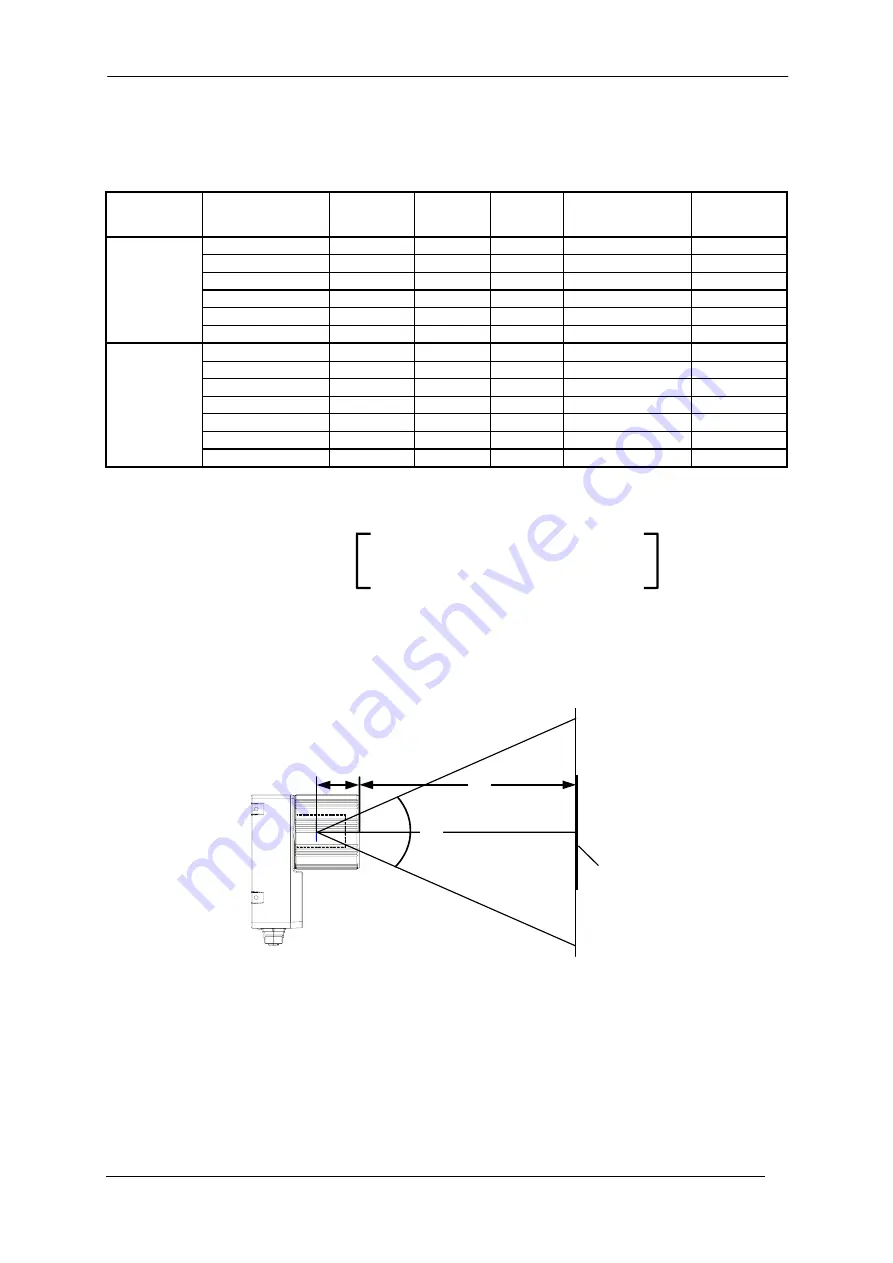
FOV
x
= 2 (d + 35 mm) tan (
α
x
/2)
where:
FOV
x
= horizontal, vertical or diagonal FOV
α
x
= horizontal, vertical or diagonal viewing angles.
d
= focus distance
d
35 mm
FOV
plane
α
Figure 18 – Reading Distance References
Example:
The FOV for a
Matrix 400-600-0x0 base
using the
16 mm lens
at a
focus distance of 200 mm
is:
FOV
H
= 2 [(200 mm + 35 mm) tan (24°/2)] =
100 mm
FOV
V
= 2 [(200 mm + 35 mm) tan (18°/2)] =
74 mm