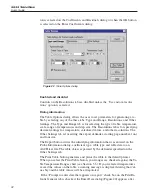
solve for two coefficients. The example below shows a set of four equations
representing data at five temperatures ( R
tpw
and resistance at four test tempera-
tures) along with the matrix method used to solve the overdetermined set.
A
Δ
Δ
W
a W
b W
W
a W
b W
T
T
T
T
T
T
1
1
1
2
2
2
2
2
1
1
1
1
=
− +
−
=
− +
−
[ (
)
(
) ]
[ (
)
(
) ]
Δ
Δ
W
a W
b W
W
a W
b W
T
T
T
T
T
T
3
3
3
2
4
4
4
2
1
1
1
1
=
− +
−
=
− +
−
[ (
)
(
) ]
[ (
)
(
) ]
B
Matrix
W
W
W
W
Matrix
W
T
T
T
T
T
1
1
2
3
4
2
1
1
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
−
Δ
Δ
Δ
Δ
(
) (
)
(
) (
)
(
) (
)
(
) (
W
W
W
W
W
W
W
T
T
T
T
T
T
T
1
2
2
2
2
3
3
2
4
4
1
1
1
1
1
1
−
−
−
−
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
1
2
)
C
Solution
Matrix
Matrix
Matrix
Matrix
T
T
=
⋅
⋅
⋅
(
)
–
2
2
1
2
1
An exact solution (i.e., two unknowns in two equations) would be arrived at
with the following operation:
C
′
Solution
Matrix
Matrix
=
⋅
2
1
1
–
3.8.2
IPTS-68
IPTS-68 Like the ITS-90, the IPTS-68 is expressed in terms of resistance ra-
tios. The denominator, however, is the resistance at the ice point (0.000C)
rather than the resistance at the triple point of water (0.010C). This software al-
lows only exact solutions for the IPTS-68 and uses iteration or simple algebra
for the solutions.
3.8.3
Callendar-Van Dusen
The Callendar-Van Dusen expression is basically a third order polynomial with
the third coefficient (
β
) set to zero above 0°C. The polynomial is expressed in
terms of resistance vs. temperature in °C. It is solved by matrix methods in a
similar manner as the ITS-90 expression shown above with temperature on the
left of the equal sign and the polynomial on the right. The software allows for
overdetermined solutions. Only data above 0°C is used for solution of the first
two coefficients (
α
and
δ
). Data both above and below 0°C is used for solution
of
β
.
3.8.4
Polynomial and thermocouple
Polynomial solutions are arrived at using matrix methods as with the ITS-90
and the Callendar-Van Dusen. Platinum probes require polynomials expressed
in terms of resistance vs. temperature. Thermistor probes exhibit exponential
resistance vs. temperature relationships and the polynomials used are exponen-
tial expressions in terms of resistance vs. temperature. The polynomials can be
of any order up to 9th for platinum probes and up to 6th for thermistor probes.
45
3 Coefficients menu
Methods used for calculating coefficients