Geonics Limited EM38-MK2, Operating Manual

13 

instrument reading in the horizontal dipole mode is more sensitive to instrument height or 
conversely that in regions where the surface topography varies rapidly on the order of 10-20 cm 
we can expect some scatter in the horizontal dipole readings. 
 
 
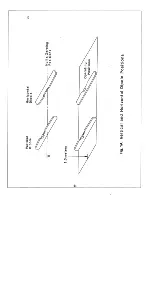
In the event that the earth is two-layered it is possible to resolve this geometry by lifting the 
EM38 above the ground and making a sequence of measurements at various heights in both the 
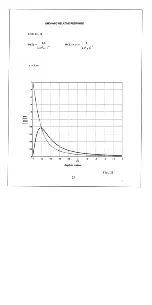
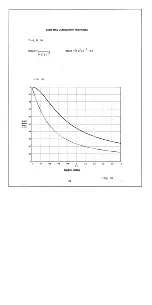
horizontal and vertical dipole mode.  The curves shown in Figs. 4 and 5 illustrate the fall-off 
with height of the apparent conductivity for a variety of two-layered configurations; to employ 
them one simply plots the measured apparent conductivity with height on a piece of transparent 
paper to the same scale as the figures and translates the plot vertically or horizontally across the 
various figures until a match is obtained.  The various layer parameters are then calculated as in 
the following example, using the measured values of apparent conductivity from Table 1. 
 
 
 

TABLE 1 

Apparent Conductivity (mS/m) 

h (m)   

Vertical 

   Horizontal 

 Dipole  

    Dipole     

  0.0 

   93 

       77 

  0.5 

   62 

       36 

  1.0 

   41 

       23 

  1.5 

   29 

       16 

  2.0 

   23 

       12 

 
 
By translating this data as described above on top of the various curves of Fig. 4 we see that 
good agreement is achieved for t=0.3 m and k=

2

/

1

=2.  Furthermore we note that, in the vertical 

dipole mode 

a

/

1

=1.85 when 

a

=93 mS/m.  Therefore 

1

=

a

/1.85=50 mS/m, 

2

=2

1

=100 

mS/m, and t=0.3 m, fully resolving the two-layered geometry. 
 
It should be noted that these curves are also useful for a three-layered earth geometry where the 
upper layer is relatively resistive compared with the other two, as illustrated in Fig. 6.  In this 
case we simply assume that 

1

=0 and that this layer effectively prevents us from laying the 

instrument on the more conductive second layer.  The fall-off with height of the apparent 
conductivity over such a geometry will still be as shown in Figs. 4 and 5 except that when a good 
match to one of these curves has been obtained it will be found that at a measured instrument 
height of zero meters the appropriate curve will still indicate a finite height, the value of which is 
the actual thickness of the upper resistive layer. 
 
 
The user is cautioned that, to the accuracy with which the measurements can be made, more than 
one set of the curves shown in Figs. 4 and 5 may match the field data, in which case he must rely 
on other factors (such as knowledge of the probable geology) to decide which model is more 
appropriate.