FAN PERFORMANCE
System Dynamics
For a given flow rate (cfm), an air distribution system
produces a resistance to airflow (Ps). This resistance is
the sum of all static pressure losses as the air flows
through the system. Resistance producing elements
include ductwork, dampers, grills, coils, etc.
A fan is simply the device that creates the pressure
differential to move air through the system.
The greater the pressure differential created by the fan,
the greater the volume of air moved through the
system. Again, this is the same principle that relates to
water pumps. The main difference in our case is that
the fan is pumping air.
Tests have established a relationship between cfm and
Ps. This relationship is parabolic and takes the form of
the following equation:
Ps = K x (cfm)
2
Where K is the constant that reflects the “steepness” of
the parabola. This equation literally states that Ps
varies as the square of the cfm.
For example, whenever the cfm doubles, the Ps will
increase 4 times. The figures on the next page
graphically illustrate this concept.
The first two sections of this guide contain information
needed to select the right fan for the particular
application. The information in this section is useful
once the fan has been selected and installed on the job.
The fan curves and system resistance curves below will
help to solve fan performance problems that may be
encountered in a variety of applications.
Fan Dynamics
A fan is simply an air pump. The rate at which a fan can
“pump” air depends on the pressure the fan must
overcome. This principle also relates to water pumps.
A water pump is able to deliver more water through a
2 in. diameter hose than a 1 in. diameter hose because
the 1 in. hose creates more resistance to flow.
For a fan, every flow rate (CFM-Cubic Feet per Minute)
corresponds to a specific resistance to flow (Ps-Static
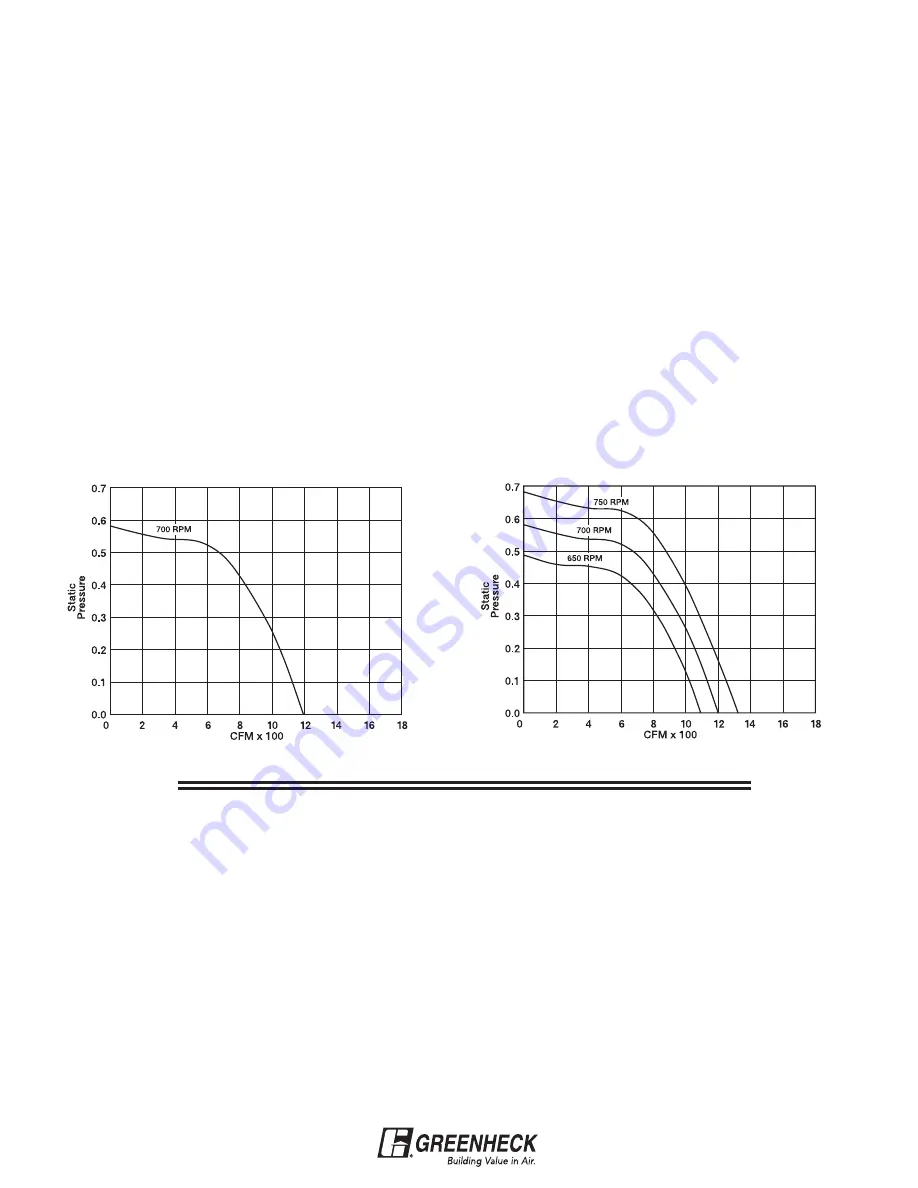
Pressure). The series of cfm, Ps points for a fan at a
constant rpm is called a fan curve. A fan curve at 700
rpm is shown below.
At 0.25 in. Ps, this fan will deliver 1000 cfm. If the
pressure increases, cfm decreases. If the pressure
decreases, cfm will increase.
At 700 rpm, the operating point will slide along the fan
curve as static pressure changes, but it will never lie off
the curve. In order for a fan to perform at a point off the
curve, the rpm must be changed.
The figure below illustrates how rpm affects the fan
curve. Notice that the general shape of the curves are
the same. Changing rpm simply moves the curve
outward or inward.
21
Fan Curve
Varying Fan Curve