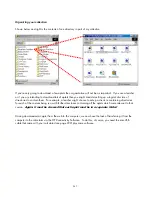
S
S
o
o
m
m
e
e
e
e
x
x
a
a
m
m
p
p
l
l
e
e
s
s
o
o
f
f
s
s
a
a
v
v
e
e
d
d
a
a
p
p
l
l
e
e
t
t
s
s
The Triangles aplet
the Solve aplet and
it under the new
name of “Triangles”. Now
In the
APLET
view,
it and enter the formulas shown.
The theta character can be obtained from the keyboard on the zero
button using
ALPHA
. Change into the
MODES
view and set the angle mode to
Degrees
(unless you want to
use another mode). By changing into the
NUM
view you can now use this to solve problems in right triangles.
Some users choose to use the letter
D
for degrees rather than theta because theta can be mistaken for an
O
.
The Prob. Distributions aplet
the Solve aplet and
it under the new
name of “Prob. Distr.”.
In the
APLET
view,
This aplet is for use by students studying probability distribution functions, and contains formulas that can be
used to perform calculations on the Binomial, Poisson, Exponential and Normal distributions. You can adapt
it to the requirements of your particular course.
the aplet and enter the formulas shown below.
Firstly,
E1: V=N!/((N-R)!*R!)*P^R*(1-P)^(N-R)
E2: V= (J=A,B, N!/((N-J)!*J!)*P^J*(1-P)^(N-J))
E3: P=e^-M*M^K/K!
E4: P= (J=A,B,e^-M*M^J/J!)
E5: P=
(A,B,K*X^3*(2-X),X)
E6: P=e^-(K*A)-e^(-K*B)
E7: P=UTPN(M,
S
2
,X)
E8: P=1-UTPN(M,S
2
,X)
E9: P=UTPN(M,S
2
,A)-UTPN(M, S
2
,B)
E0: P=UTPN(M,S
2
,M-K)+ UTPN(M,S
2
,M+K)
These formulas can be used in the
NUM
view to solve problems involving the probability distributions listed
earlier. Some explanations and examples are given on the next page.
Note that equations
E1
and
E2
use the expression
N!/((N-R)!*R!)
instead of
COMB(N,R)
because doing this
allows backward solving to solve for
N
. Using
COMB(N,R)
only allows the formula to be used in a forward
direction. The drawback of this is that values of
N
above roughly 75 will cause overflow internally and result
in errors. However, values like this should probably be done using a Normal approximation anyway. If this is
a problem, replace the
COMB(N,R)
. Additionally, the letter
V
for value is used in these two equations
because, for this particular distribution, the variable
P
has the specific meaning of “the probability of
individual success”.
232