Equation
E6
(
≤ ≤
)
for an exponential distribution. To calculate
P x
a
)
use
P
(
0
≤ ≤
)
. To
calculate
P x
a
)
just find
P x
a
)
and then use the
HOME
view to calculate the complement.
This equation gives
P a
x
b
(
≤
x
a
(
≥
(
≤
Equations
E7
and
E8
Finally, equations
E7
to
E0
concern the Normal distribution, with
E7
giving
P X x
(
≤
)
,
(
≥
)
,
E8
giving
P X x
(
≤ ≤
)
and
E0
allowing calculation of questions such as “what distance either side of the
E9
giving
P a
x
b
mean will give a probability of 0.45?”.
Finally, you may choose to split this aplet into two, placing equations 1 to 4 into an aplet called “
Discrete
PDFs
” and the others into another called “
Cont. PDFs
”. I encourage my students to do this because it
reinforces the correct technique of first of identifying whether the problem is discrete or continuous.
The Transformer aplet
This aplet is based on the Parametric aplet and allows students to
investigate geometric transformations using 2x2 matrices.
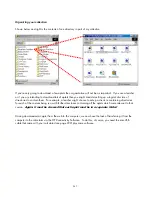
In the
APLET
view,
the Parametric aplet and
it under the
new name of “Transformer”. Enter the equations shown right.
Change to the
PLOT SETUP
view
and enter the settings shown.
Now change to the
Matrix Catalog
view and enter the matrices shown
below into
M1
and
M2
.
⎡
1
0
⎤
⎡
1 2
1 1
⎤
M
2
=
⎢
⎢
1 1
3 1
⎥
⎥
M
1
=
⎢
⎢
0
−
1
⎥
⎥
⎣
⎦
⎣
⎦
234