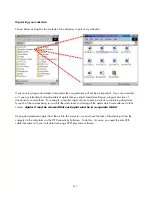
Change to the
HOME
view and perform the calculation shown right and
finally press
PLOT
.
The result is a triangle with corners at (1,1), (2,1) and (1,3), along with
its image after reflection in the x axis.
matrix
M1
so that it contains another matrix.
We can now
⎡
−
1 0
⎤
For example:
⎢
⎢
0
1
⎥⎦
⎥
⎣
To see the effect of this new matrix, simply return to the
HOME
view,
the previous calculation and press
ENTER
. The new image will
be stored into matrix
M3
. If you now return to the
PLOT
view the image
will not appear to have changed as the aplet does not realize the matrix
has changed but pressing
PLOT
again will force a re-draw of the new image.
The great power of this aplet is its use as a teaching and investigative
tool. Simply continue to
matrix
M1
, repeating the
HOME
calculation, and re-
PLOT
ing each time to see the change in the image.
For teachers, the degree of guidance which should be given to a class will obviously depend on their level of
ability. For an able class you might choose to give no more guidance than to suggest that they confine their
investigations initially to placing numbers only on the diagonals. It may be a good idea to challenge them to
record their matrices on the board as they discovered them. For a less able class you might hand out a list of
matrices they should investigate. Perhaps in the form of a set of cards with matrices and geometric trans
formations which must be matched up. A highly able class will find nearly all relevant matrices within 20 to
30 minutes. A less able class may need considerable guidance.
So… how does this aplet work?
The formulas in the
SYMB
view form the key to the process by allowing
the calculator to fetch values from the matrices, with the values fetched
being determined by the settings in the
PLOT SETUP
view.
For example, as
T
runs from
1
to
4
in steps of
1
the
(X1,Y1)
values
plotted become (
M2(1,1)
,
M2(2,1)
), (
M2(1,2)
,
M2(2,2)
),
(
M2(1,3)
,
M2(2,3)
) and (
M2(1,4)
,
M2(2,4)
). If we now substitute the
actual values from matrix
M2
then these points become (1,1), (2,1),
(3,1) and (1,1), which give the shape when plotted.
235