42
A
A
P
P
P
P
E
E
N
N
D
D
I
I
X
X
A
A
:
:
S
S
O
O
M
M
E
E
W
W
O
O
R
R
K
K
E
E
D
D
E
E
X
X
A
A
M
M
P
P
L
L
E
E
S
S
The examples which follow are intended to illustrate the ways in which the calculator can be used to help
solve some typical problems. In some cases more than one method is shown. In some cases the method is
chosen more to illustrate the capabilities of the calculator than because it is necessarily the most efficient
method. Sometimes these problems are quoted elsewhere in the book and repeated here for convenience.
F
F
i
i
n
n
d
d
i
i
n
n
g
g
t
t
h
h
e
e
i
i
n
n
t
t
e
e
r
r
c
c
e
e
p
p
t
t
s
s
o
o
f
f
a
a
q
q
u
u
a
a
d
d
r
r
a
a
t
t
i
i
c
c
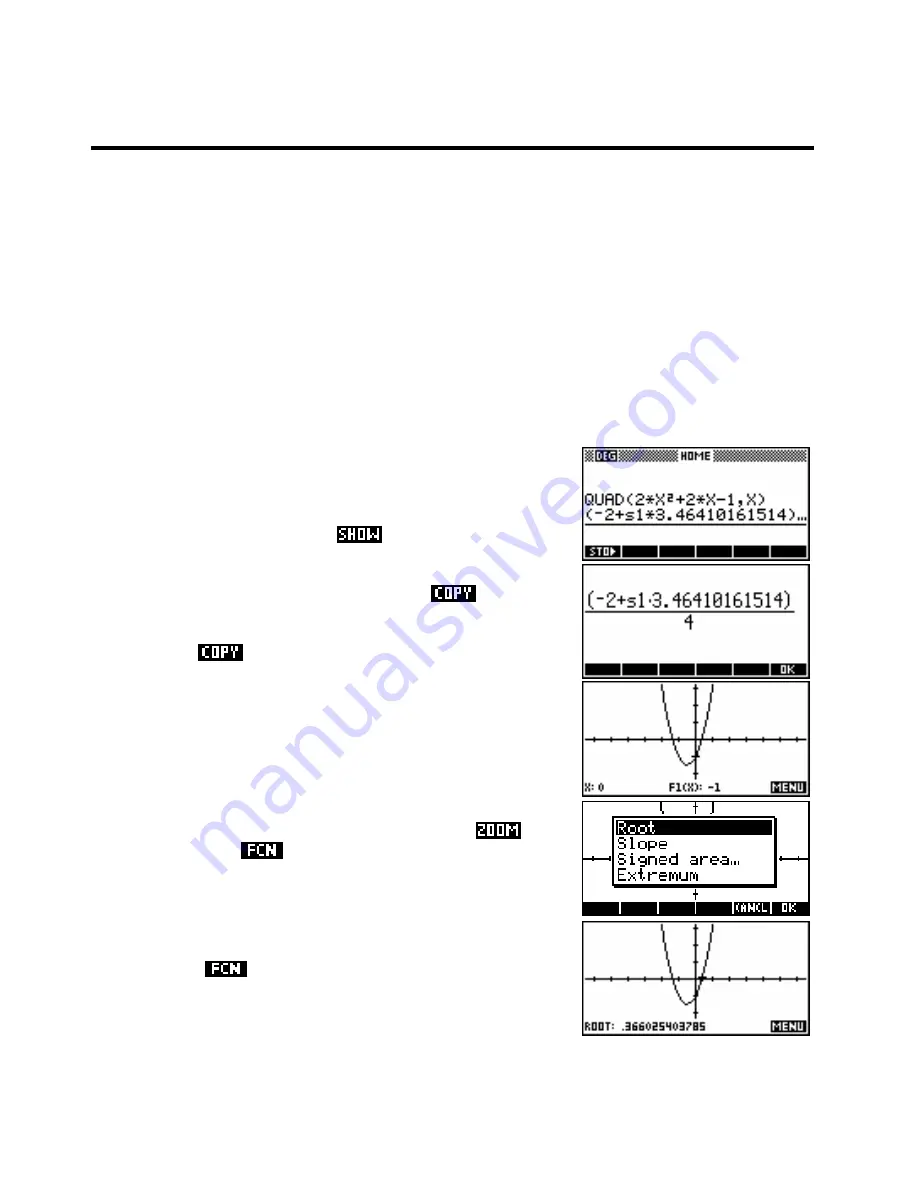
Find the x intercepts of the quadratic equation
g x
=
( ) 2
x
2
+
2
x
−
1
Method 1 - Using the
QUAD
function in
HOME
.
key in the bottom view.
This is probably not a method that one would use in general but it has
the slight advantage that the answer is given in the same form that you
would see it if you used the Quadratic formula. Just
This method is shown right, using the
the result,
edit and square the decimal part to find the value of the discriminant if
you need the result in surd format. The ‘
S1
’ is the calculator’s version of
the ± sign. Just
the result and remove the S1 to obtain the
positive solution, replacing the + with a - to obtain the other. This method
is only of use if the question said “Show working” because it doesn’t
give the answer directly.
Method 2 - Using the Function aplet.
Shown right. Enter the function into the
SYMB
view, use the
VIEWS
key
and choose ‘
Decimal
’. If the axes don’t suit, then use the
options. Now use the
option of
Root
to find the two roots. One
result is shown.
This is clearly the best method and has the advantage that you can see
the graph clearly.
Root
method does not depend on the graph
being on the screen. The algorithm will still find roots even if they are
not currently visible.
Note: Using the
298













































