I want to graph this function for the first six seconds but I am not sure
what y scale to use so I will set
XRng
to be 0 to 6 in the
PLOT SETUP
view and then choose
VIEWS
-
Auto Scale
. The result is shown right.
Extremum
, I find that the time of closest approach is at
t =
Using
3.4 hours
(3:24 pm) with a separation at that time of
d = 1.3416 km
.
The y axis has been adjusted slightly to make the x axis visible.
C
C
i
i
r
r
c
c
u
u
l
l
a
a
r
r
M
M
o
o
t
t
i
i
o
o
n
n
a
a
n
n
d
d
t
t
h
h
e
e
D
D
o
o
t
t
P
P
r
r
o
o
d
d
u
u
c
c
t
t
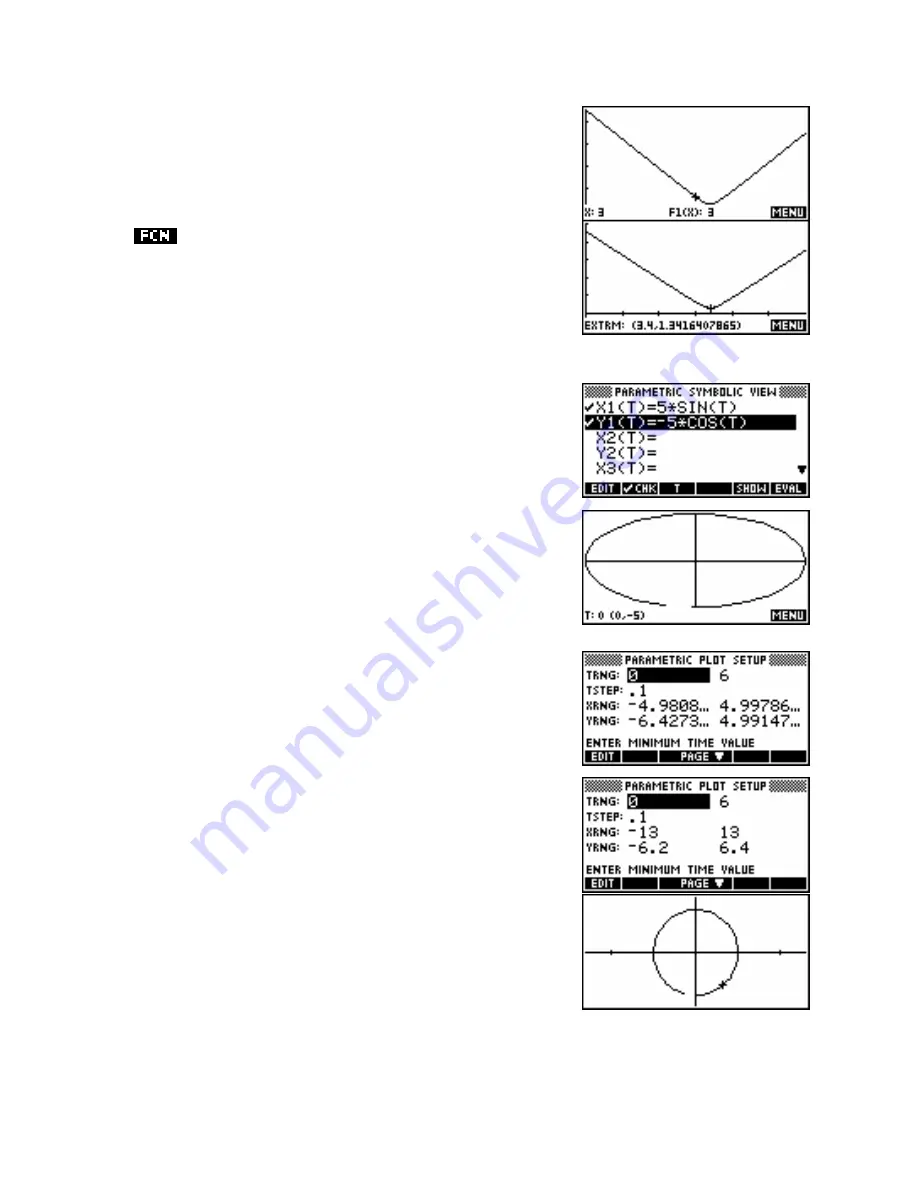
A particle’s position at time t seconds is given by
r
=
5sin
θ
i
−
5 cos
θ
j
. Draw a sketch of its path for the first 6
seconds of movement. Show that its path is circular.
The first step is to graph the particle’s path. We go into the Parametric
aplet and enter the rule into the first equation
X1
,
Y1
.
After setting
TRng
to 0 to 6 and then using
VIEWS
-
Auto Scale
we get
a result which is does not look like a circle, but this may be due to
distortion through not using a ‘square’ screen.
If we inspect the
PLOT SETUP
view, we can see that the settings are
nearly double those of the default ‘square’ screen of -6.5 to 6.5 and -
3.1 to 3.2 In the
PLOT SETUP
view, press
SHIFT CLEAR
to set
everything back to default, then double each setting for the x and y axes
and set
TRng
back to 0 to 6.
Pressing
PLOT
again will make it clear visually that this is a circle and
we can copy this diagram onto our test paper as the required graph.
Note the gap at the bottom because the
TRng
stops at 6 instead of 2
π
.
Of course, this is not really a proof of circularity!
311
















































