A
A
r
r
e
e
a
a
U
U
n
n
d
d
e
e
r
r
C
C
u
u
r
r
v
v
e
e
s
s
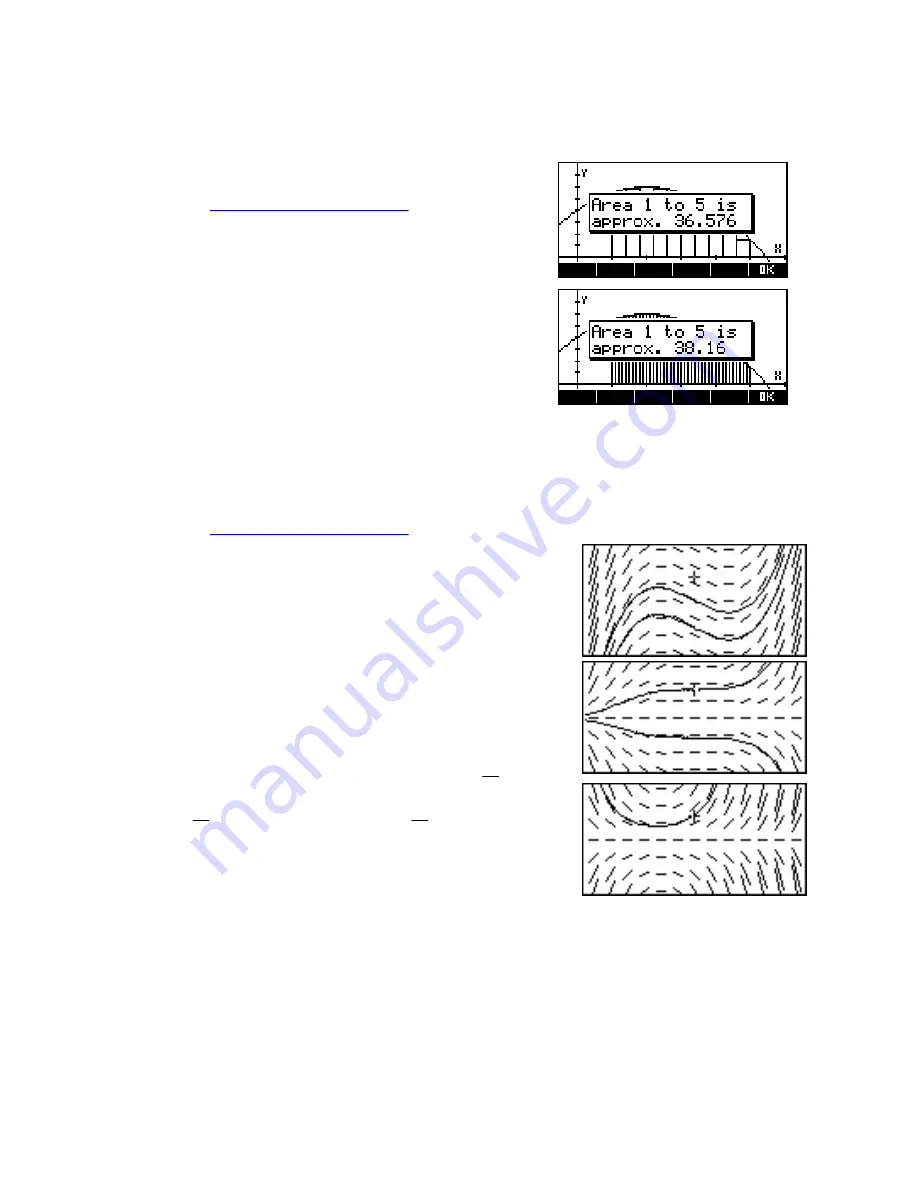
This topic is most easily handled using an aplet from
The HP HOME
View
web site (at
http://www.hphomeview.com
). This aplet, called
“Curve Areas” will draw rectangles either over or under a curve or
use trapezoids. A number of curves are supplied pre-set but the user
can also enter their own. The user can nominate the interval width
and the number of rectangles.
Most importantly, a worksheet is bundled with the aplet which will
lead the student through the process of deducing an area function
and hence to the anti-differentiation of
x
n
.
F
F
i
i
e
e
l
l
d
d
s
s
o
o
f
f
S
S
l
l
o
o
p
p
e
e
s
s
a
a
n
n
d
d
C
C
u
u
r
r
v
v
e
e
F
F
a
a
m
m
i
i
l
l
i
i
e
e
s
s
One of the concepts which students find quite difficult to come to grips with is that of sketching a field of
slopes from a derivative function and, from this, sketching a family of curves. An aplet from
The HP HOME
View
web site (at
http://www.hphomeview.com
), called “Slope Fields”, will assist with this process.
In this aplet the user enters the derivative function into
F1(X)
and then
uses the
VIEWS
menu to produce a field of slopes. A cross-hair is
projected onto the field which the user can move around. When the
user presses
ENTER
, a curve is drawn, starting at that point and
projecting to the right and then the left, and following the field of slopes.
Repetition of this will illustrate the fact that there are a family of curves,
separated by a constant, which all fit the ‘description’ of the function
stored in
F1(X)
.
2
⎞
The screen shots to the right are the result of
F1(X)=X
2
+1
⎛
⎜
dy
=
x
+
1
⎟
,
⎝
dx
⎠
2
⎞
F1(X)=X
2
*Y
⎛
dy
=
x y
⎟
and
F1(X)=(X+1)*Y
⎛
dy
=
(
x
+
1
)
y
⎟
⎞
⎜
⎝
dx
⎠
⎝
⎜
dx
⎠
respectively.
320
















































