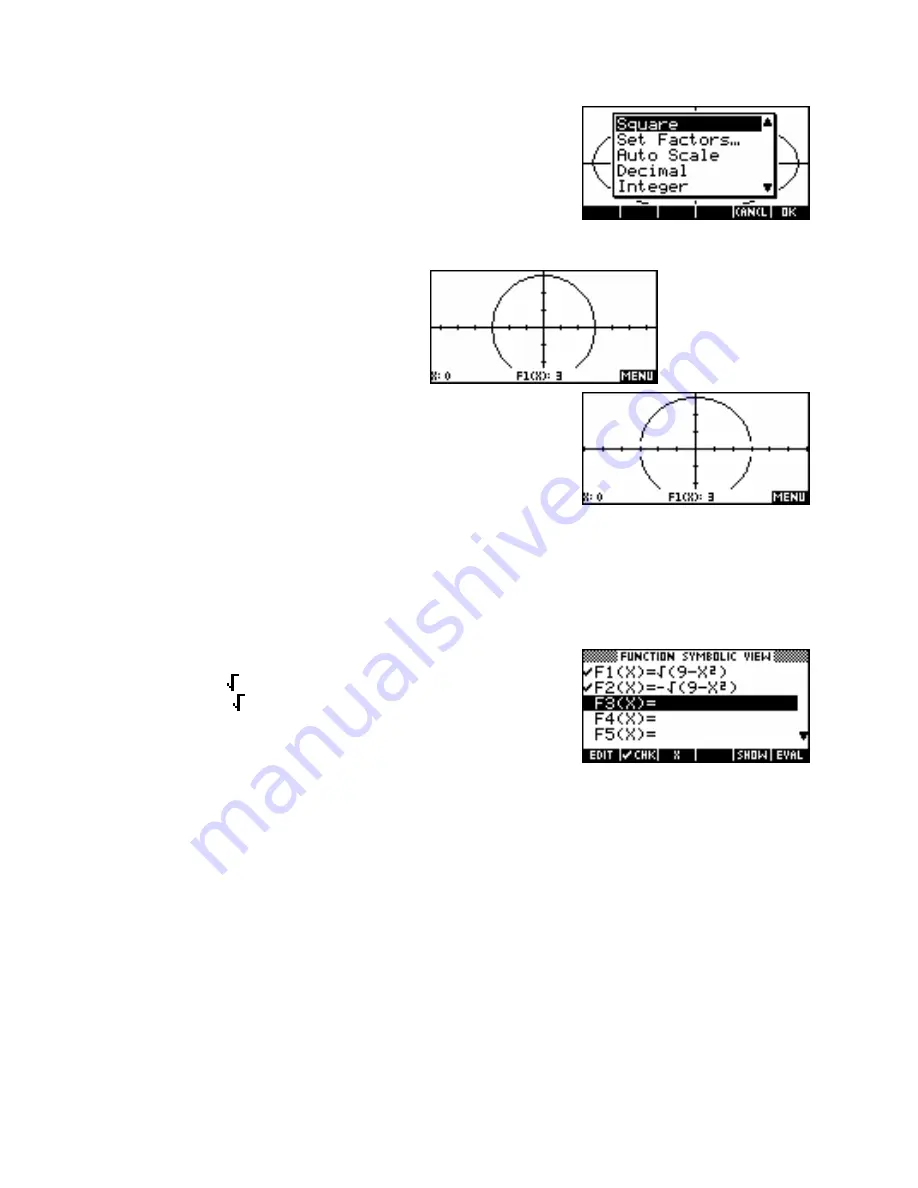
The simplest way to deal with this is to use scales which are multiples of
13
x
the default scales. For example by using
− ≤ ≤
13
and
6.2
y
6.4
−
≤ ≤
. These are a scale factor of 2 from the default axes of
6.5
x
3.1
y
3.2
.
−
≤ ≤
6.5
and
−
≤ ≤
You can also use the
Square
option on the
ZOOM
menu. This adjusts the
y
axis so that it is ‘square’ relative to whatever
x
axis you have chosen.
The second issue is caused by the domain of the
circle being undefined for some values. The
screen on your calculator is made up of small
dots called pixels and is 131 pixels wide and 64
pixels high. As was mentioned earlier, this means
that each pixel is 0.1 apart on the x and y axes.
This can affect your graphs and it becomes particularly obvious with
circles because the graph does not exist for the part of the x axis outside
the circle. The two screen shots right are an example of two images of
2
the same graph
x
2
+
=
9
using two slightly different scales. You can see that the second example has
y
missing pieces.
2
Let's look at the circle
x
2
+
=
9
as an example. This circle only exists from -3 to 3 on the x axis and is
y
undefined outside this domain. In order to graph it you have to rearrange it into two equations of:
F1(X)= (9-X
2
)
for the top half
&
F2(X)= - (9-X
2
)
for the bottom half.
If you enter these equations and then graph them with the default axes then you get a perfect circle.
However, if you change the x axis to -6 to 6 rather that the default setting and then
PLOT
again you will find
that part of the circle disappears. This is shown in the second snapshot above.
The reason for this is that when the calculator draws the graph it does so by ‘joining the dots’. For the default
scale of -6.5 to 6.5 this is not a problem since the edges of the two half circles at -3 and 3 fall on a pixel. This
means that the last segment of the graph plotted extends is from 2.9 to 3 and the circle reaches right down to
the x axis.
68
















































