Page 5-26
If you press
µ
you will get:
‘(X^6+8*X^5+5*X^4-50*X^3)/(X^7+13*X^6+61*X^5+105*X^4-45*X^3-
297*X^2-81*X+243)’
The FROOTS function
The function FROOTS obtains the roots and poles of a fraction. As an
example, applying function FROOTS to the result produced above, will result
in: [1 –2. –3 –5. 0 3. 2 1. –5 2.]. The result shows poles followed by their
multiplicity as a negative number, and roots followed by their multiplicity as a
positive number. In this case, the poles are (1, -3) with multiplicities (2,5)
respectively, and the roots are (0, 2, -5) with multiplicities (3, 1, 2),
respectively.
Another example is: FROOTS(‘(X^2-5*X+6)/(X^5-X^2)’)= [0 –2.1 –1.3 1.2
1.]. i.e., poles = 0 (2), 1(1), and roots = 3(1), 2(1). If you have had Complex
mode selected, then the results would be:
[0 –2. 1 –1. ‘-((1+i*
√
3)/2’ –1. ‘-((1-i*
√
3)/2’ –1.].
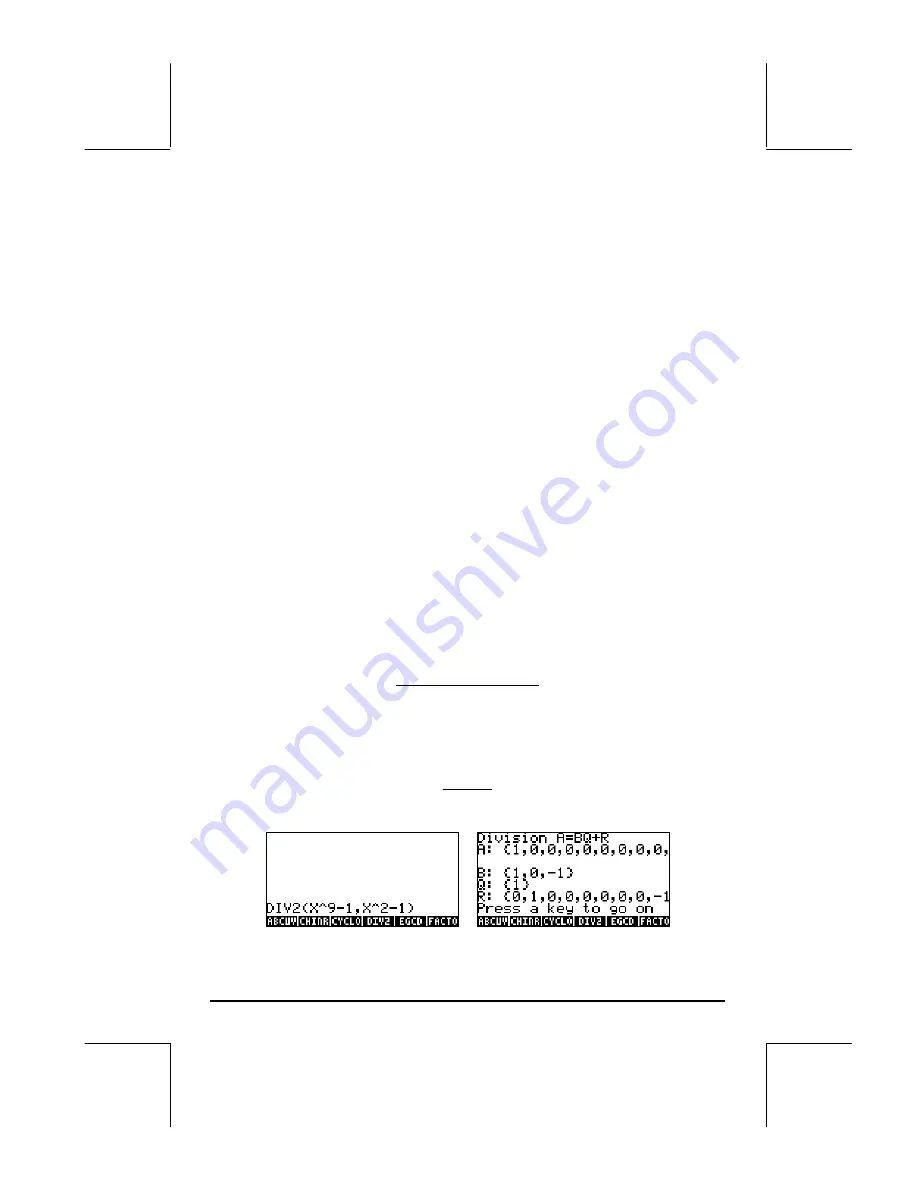
Step-by-step operations with polynomials and fractions
By setting the CAS modes to Step/step the calculator will show simplifications
of fractions or operations with polynomials in a step-by-step fashion. This is
very useful to see the steps of a synthetic division. The example of dividing
2
2
3
5
2
3
−
−
+
−
X
X
X
X
is shown in detail in Appendix C. The following example shows a lengthier
synthetic division:
1
1
2
9
−
−
X
X














































