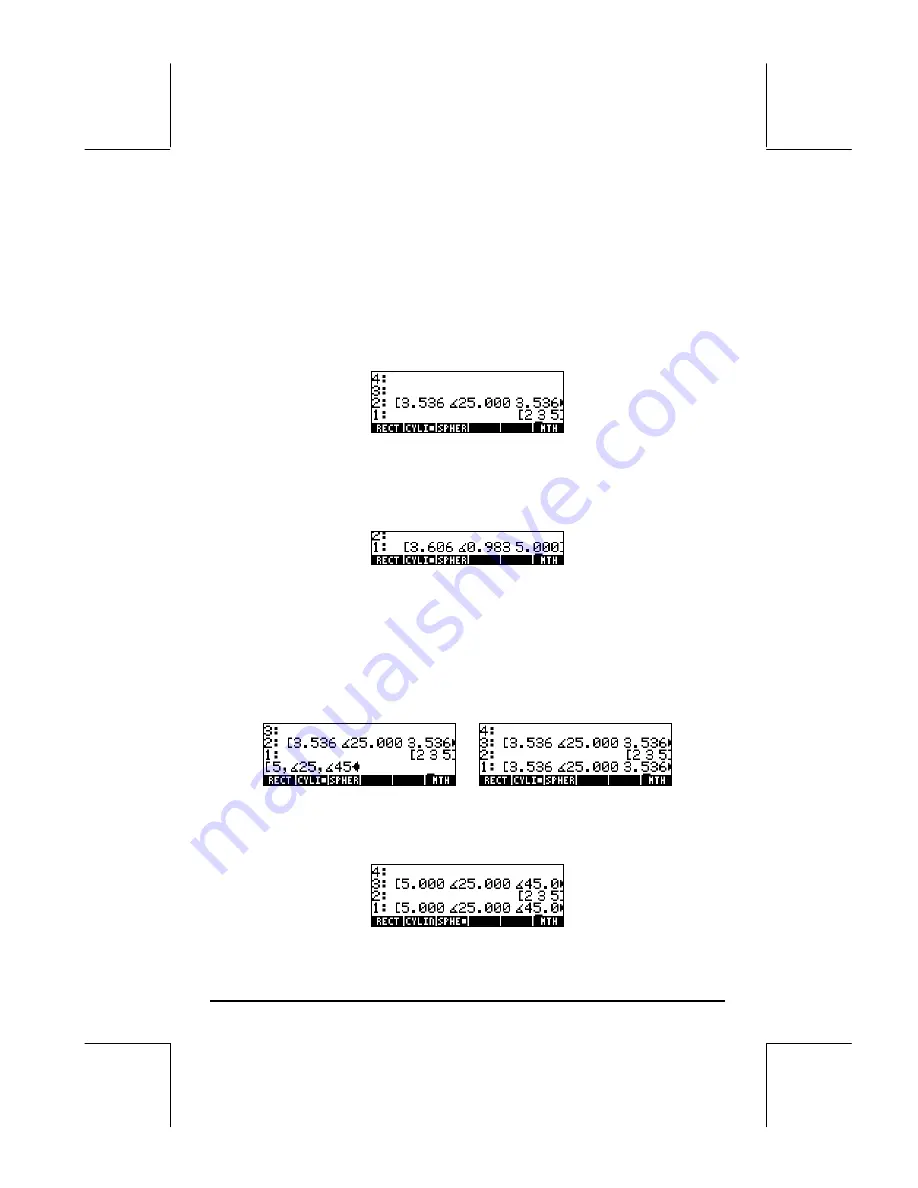
Page 9-15
The conversion from Cartesian to cylindrical coordinates is such that r =
(x
2
+y
2
)
1/2
,
θ
= tan
-1
(y/x), and z = z. For the case shown above the
transformation was such that (x,y,z) = (3.204, 2.112, 2.300), produced
(r,
θ
,z) = (3.536,25
o
,3.536).
At this point, change the angular measure to Radians. If we now enter a
vector of integers in Cartesian form, even if the CYLINdrical coordinate system
is active, it will be shown in Cartesian coordinates, e.g.,
This is because the integer numbers are intended for use with the CAS and,
therefore, the components of this vector are kept in Cartesian form. To force
the conversion to polar coordinates enter the vector components as real
numbers (i.e., add a decimal point), e.g., [2., 3., 5.].
With the cylindrical coordinate system selected, if we enter a vector in
spherical coordinates it will be automatically transformed to its cylindrical
(polar) equivalent (r,
θ
,z) with r =
ρ
sin
φ
,
θ
=
θ
, z =
ρ
cos
φ
. For example, the
following figure shows the vector entered in spherical coordinates, and
transformed to polar coordinates. For this case,
ρ
= 5,
θ
= 25
o
, and
φ
= 45
o
,
while the transformation shows that r = 3.563, and z = 3.536. (Change to
DEG):
Next, let’s change the coordinate system to spherical coordinates by using
function SPHERE from the VECTOR sub-menu in the MTH menu. When this
coordinate system is selected, the display will show the R
∠∠
format in the top
line. The last screen will change to show the following:















































