Page 11-12
The determinant of a matrix
The determinant of a 2x2 and or a 3x3 matrix are represented by the same
arrangement of elements of the matrices, but enclosed between vertical lines,
i.e.,
33
32
31
23
22
21
13
12
11
22
21
12
11
,
a
a
a
a
a
a
a
a
a
a
a
a
a
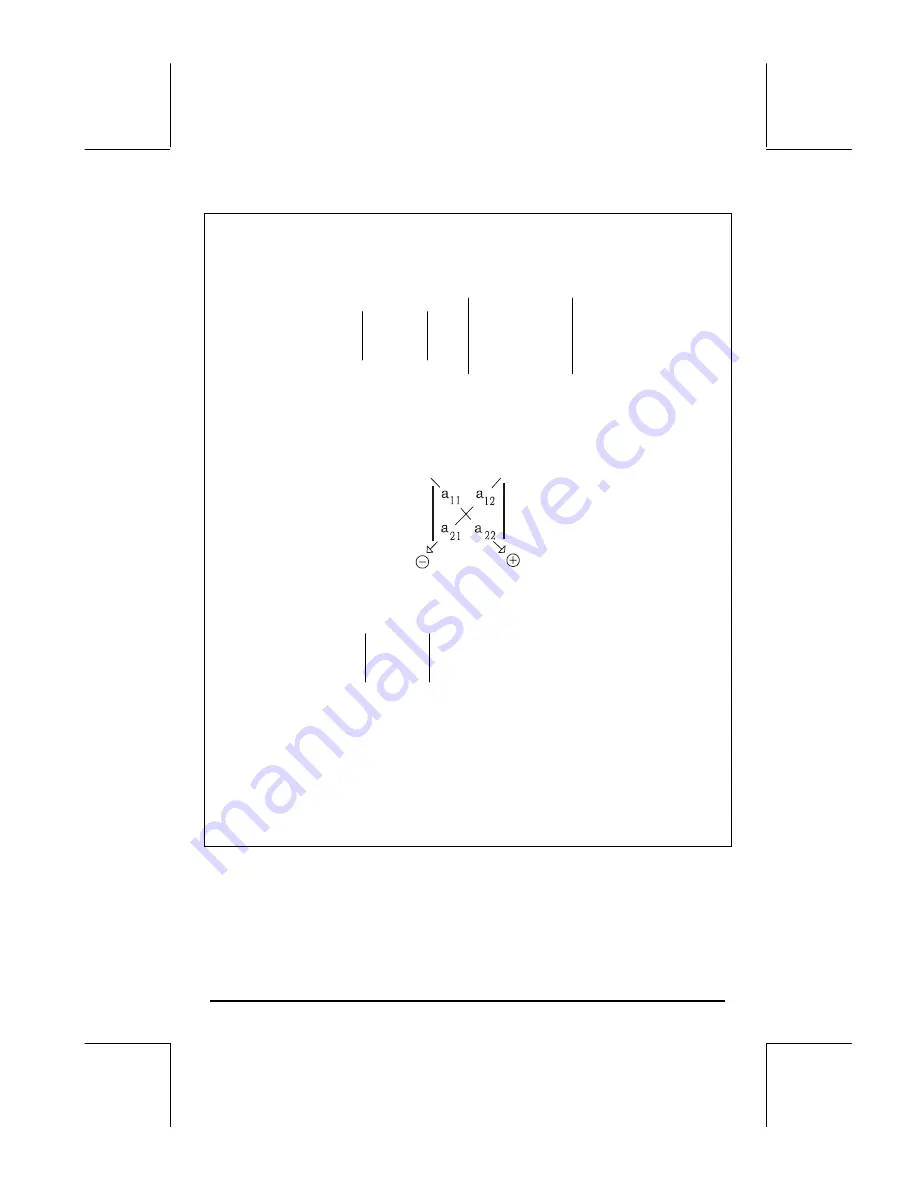
A 2
×
2 determinant is calculated by multiplying the elements in its diagonal
and adding those products accompanied by the positive or negative sign as
indicated in the diagram shown below.
The 2
×
2 determinant is, therefore,
21
12
22
11
22
21
12
11
a
a
a
a
a
a
a
a
⋅
−
⋅
=
A 3
×
3 determinant is calculated by
augmenting
the determinant, an operation
that consists on copying the first two columns of the determinant, and placing
them to the right of column 3, as shown in the diagram below. The diagram
also shows the elements to be multiplied with the corresponding sign to attach
to their product, in a similar fashion as done earlier for a 2
×
2 determinant.
After multiplication the results are added together to obtain the determinant.






































