Page 11-40
Based on the equation
A
-1
=
C
/det(
A
), sketched above, the inverse matrix,
A
-1
, is not defined if
det
(
A
) = 0. Thus, the condition
det
(
A
) = 0 defines also a
singular matrix.
Solution to linear systems using calculator functions
The simplest way to solve a system of linear equations,
A
⋅
x
=
b
, in the
calculator is to enter
b
, enter
A
, and then use the division function /. If the
system of linear equations is over-determined or under-determined, a
“solution” can be produced by using Function LSQ (Least-SQuares), as shown
earlier. The calculator, however, offers other possibilities for solving linear
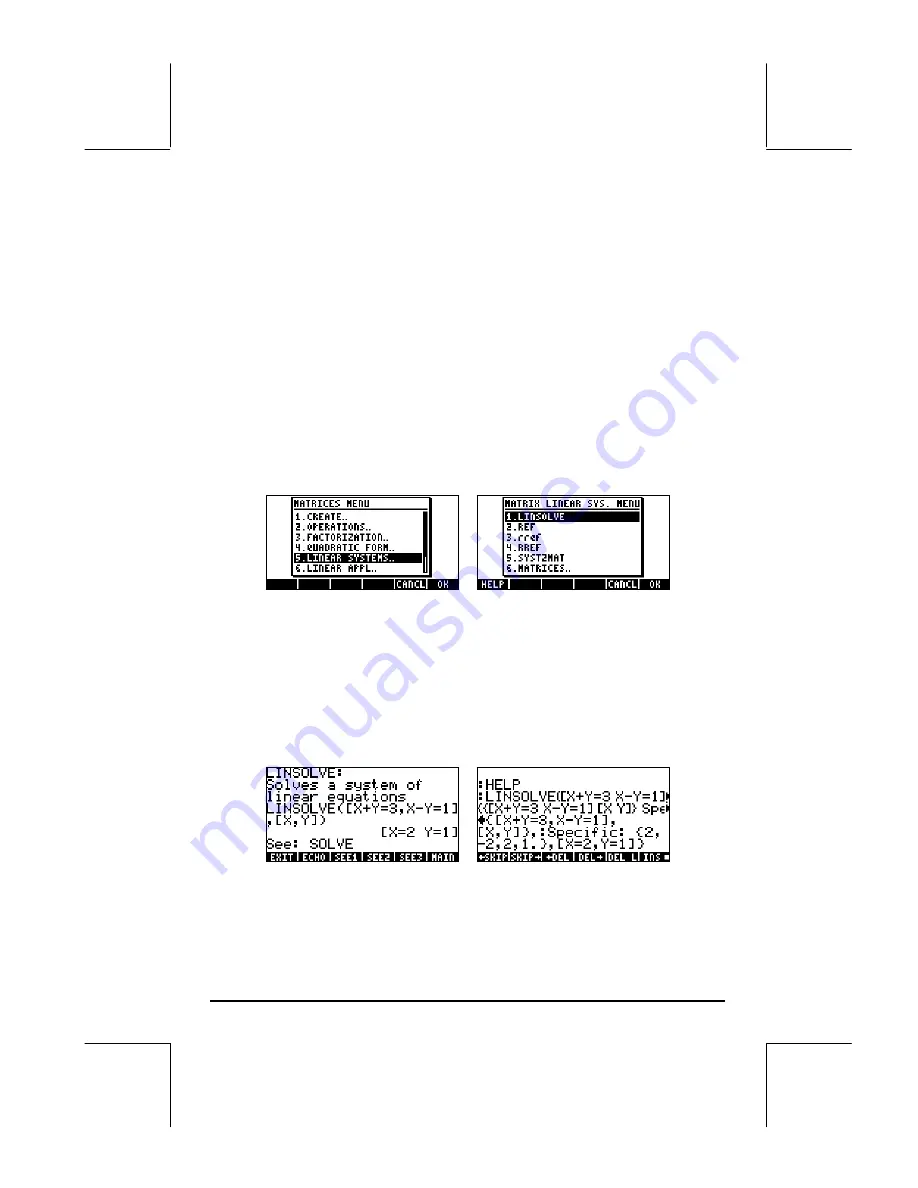
systems of equations by using Functions included in the MATRICES’ LINEAR
SYSTEMS.. menu accessible through
„Ø
(Set system flag 117 to
CHOOSE boxes):
The functions included are LINSOLVE, REF, rref, RREF, and SYST2MAT.
Function LINSOLVE
Function LINSOLVE takes as arguments an array of equations and a vector
containing the names of the unknowns, and produces the solution to the linear
system. The following screens show the help-facility entry (see Chapter 1) for
function LINSOLVE, and the corresponding example listed in the entry. The
right-hand side screen shows the result using the line editor (press
˜
to
activate):
Here is another example in ALG mode. Enter the following:
LINSOLVE([X-2*Y+Z=-8,2*X+Y-2*Z=6,5*X-2*Y+Z=-12],
[X,Y,Z])
















































