Page 16-8
dy/dx + x
2
⋅
y(x) = 5.
In the calculator use:
'd1y(x)+x^2*y(x)=5'
`
'y(x)'
`
DESOLVE
The solution provided is {‘y =
(INT(5*EXP(xt^3/3),xt,x)+cC0)*1/EXP(x^3/3))’ }, i.e.,
The variable ODETYPE
You will notice in the soft-menu key labels a new variable called
@ODETY
(ODETYPE). This variable is produced with the call to the DESOL function and
holds a string showing the type of ODE used as input for DESOLVE. Press
@ODETY
to obtain the string “
1st order linear
”.
Example 2 -- Solve the second-order ODE:
d
2
y/dx
2
+ x (dy/dx) = exp(x).
In the calculator use:
‘
d1d1y(x)+x*d1y(x) = EXP(x)
’
`
‘
y(x)
’
`
DESOLVE
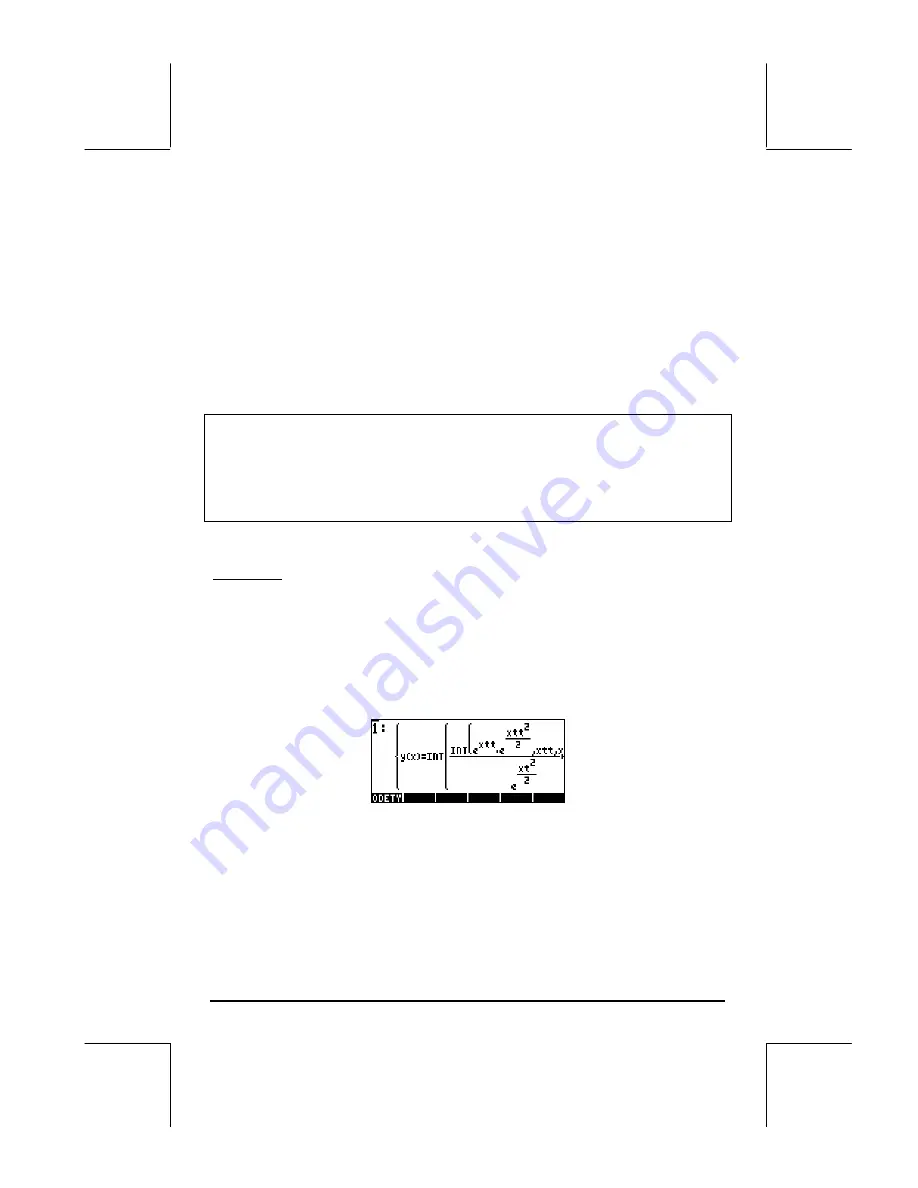
The result is an expression having two implicit integrations, namely,
For this particular equation, however, we realize that the left-hand side of the
equation represents d/dx(x dy/dx), thus, the ODE is now written:
d/dx(x dy/dx ) = exp x,
and
x dy/dx = exp x + C.
(
)
.
)
3
/
exp(
5
)
3
/
exp(
)
(
0
3
3
cC
dx
x
x
x
y
+
⋅
⋅
⋅
−
=
∫
















































