- 60 -
Copyright L
EXIBOOK
2002
GB
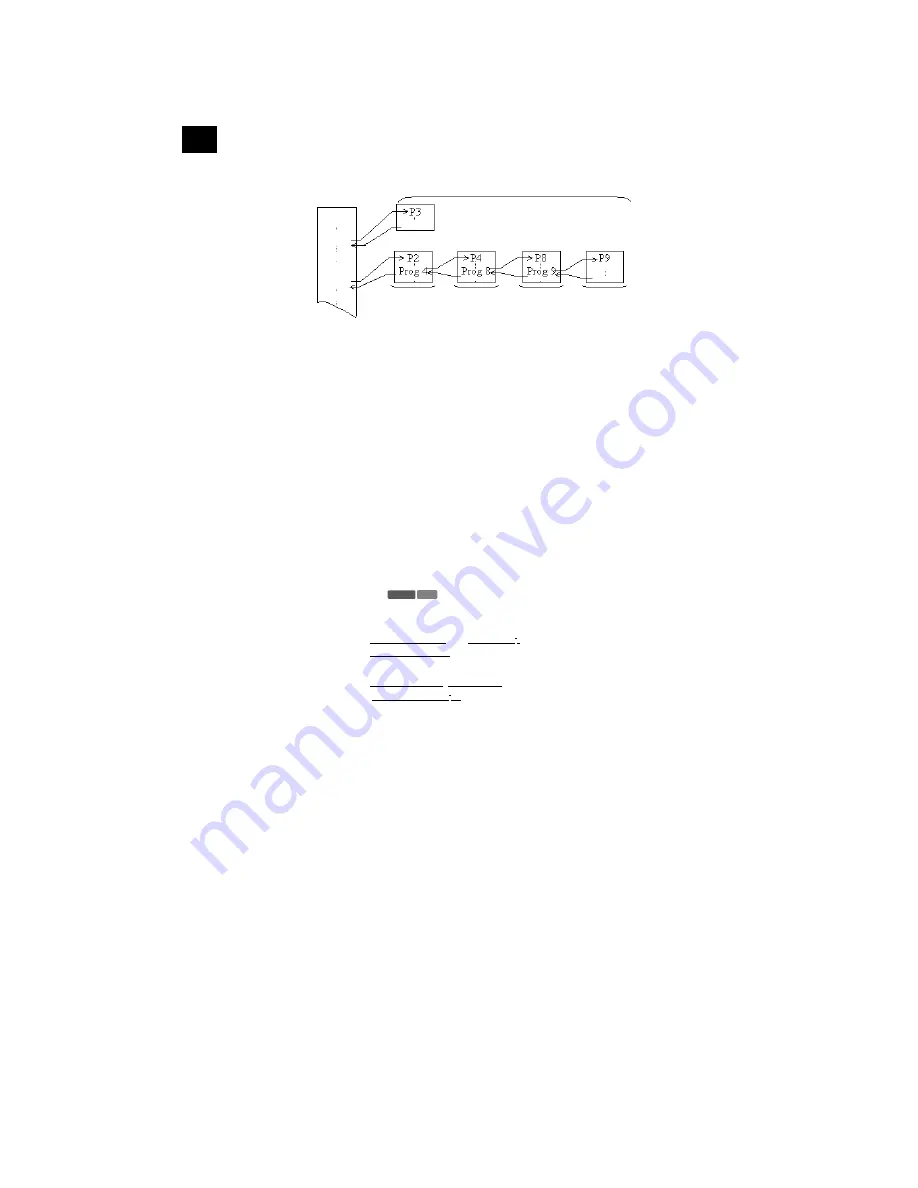
The subroutine command is “Prog” followed by a number from 0 through 9 which indicates the program
area.
Example :
Prog 0 ......... Jump to program area 0
Prog 2. ........ Jump to program area 2
After the jump is performed using the Prog. command, execution continues from the beginning of the
program stored in the specified program area. After execution reaches the end of the subroutine, the
program returns to the statement following the Prog n command in the original program area. Jumps can
be performed from one subroutine to another, and this procedure is known as “nesting”. Nesting can be
performed to a maximum of 10 levels, and attempts to exceed this limit will cause an error (Ne ERROR)
to be generated. Attempting to use Prog to jump to a program area in which there is no program stored will
also result in an error (Go ERROR).
*** A Goto n contained in a subroutine will jump to the corresponding Lbl n contained in that program
area.
Example: Simultaneously execute the two previously presented programs to calculate the surface
areas and volumes of a regular octahedron and tetrahedron.
Express the result in three decimal places.
This example employs two previously explained programs, and the first step is to input the specified
number of decimal places (
3)
Now let’s review the two original program.
Regular octahedron
P0
Fix, 3, :, ?,
→
, A, :, 2, x,
√
, 3, x, A, x
2
,
,
√
, 2,
÷
, 3, x, A, xy, 3
23 steps
Regular tetrahedron
P1
Fix, 3, :, ?,
→
, A, :,
√
, 3, x, A, x2,
,
√
, 2,
÷
, 1, 2, x, A, x
y
, 3
22 steps
Total: 45 steps
If the two programs are compared, it is evident that the underlined portions are identical. If these portions
are incorporated into a common subroutine, the programs are simplified and the number of steps required
is decreased.
Furthermore, the portions indicated by the wavy line are not identical as they stand, but if P1 is modified
to:
√
, 2,
÷
, 3, x, A, x
y
, 3,
÷
, 4, the two portions become identical.
Now the portions underlined by the straight line will be stored as an independent routine in P9 and those
underlined with the wavy line will be stored in P8.
P9
Fix, 3, :, ?,
→
, A, :,
√
, 3, x, A, x
2
,
12 steps
P8
√
, 2,
÷
, 3, x, A, xy, 3
8 steps
After the common segments have been removed, the remainder of the regular octahedron formula is stored
in P0, and that of the regular tetrahedron is stored in P1. Of course, the “Prog 9” and “Prog 8” must be
added to jump to subroutines P9 and P8.
P0
Prog, 9, :, Ans, x, 2,
, Prog, 8
9 steps
P1
Prog, 9,
, Prog, 8, :, Ans,
÷
, 4
9 steps
Total: 38 steps
With this configuration, execution jumps to program P9 at the beginning of programs P0 and P1, three
decimal places are specified, the value for one side is entered, and the surface area of the tetrahedron is
calculated. The expression “2x” of the original octahedron formula was omitted in P9, so when execution
returns to P0, “Ansx2” is used to obtain the surface of the octahedron.
7
MODE
Main routine
P0
Prog 3
Prog 2
Level 1
Level 2
Level 3
Level 4





































