Chapter 15. The PID functions
15-4
15.2.1.2
Integral operation (I action)
1) With integral operation, the manipulate value (MV) is increased or decreased
continuously in accordance time in order to eliminate the deviation between the SV
and PV. When the deviation is very small, the proportional operation can not
produce a proper manipulate value and an offset remains between PV and SV. The
integral operation can eliminate the offset value even the deviation is very small.
2) The period of the time from when the deviation has occurred in I action to when the
MV of I action become that of P action is called Integration time and represented as
Ki.
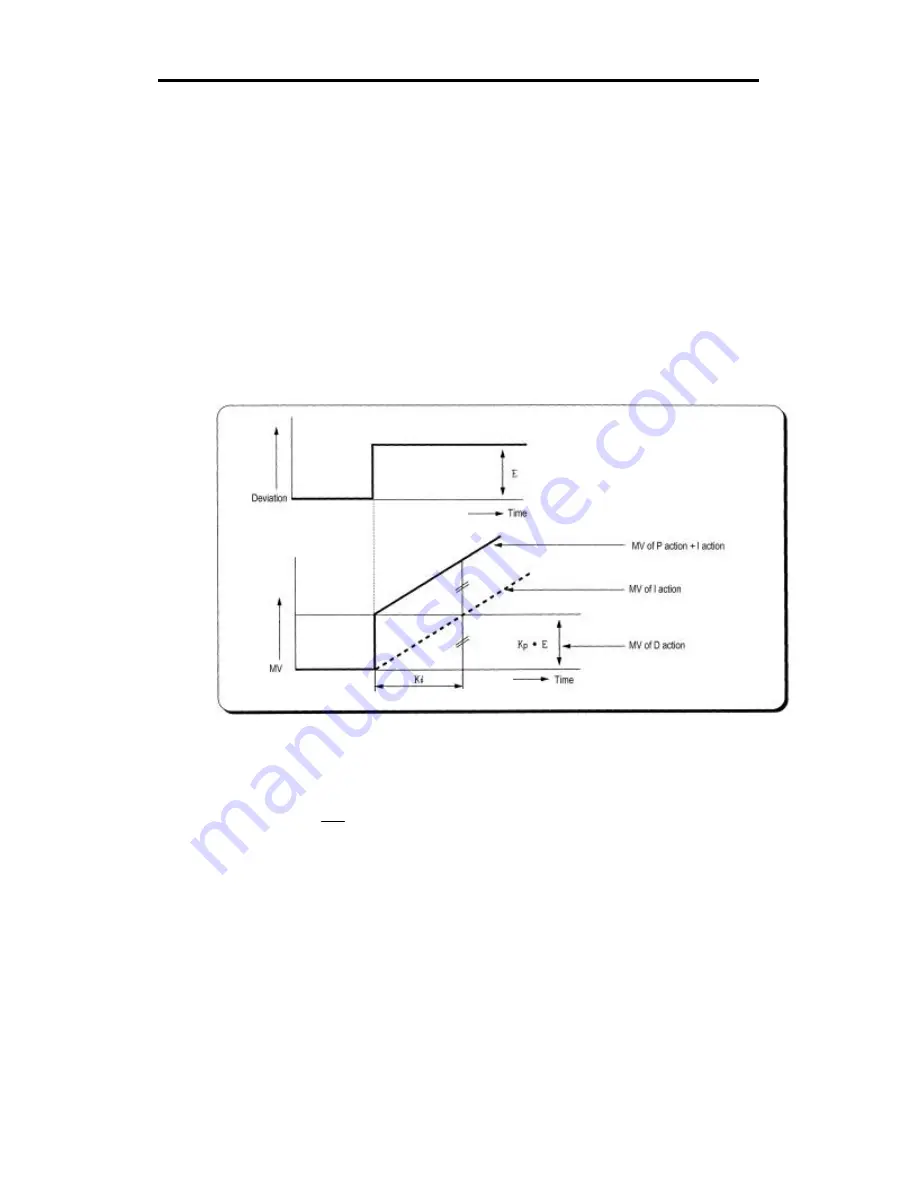
3) Integral action when a constant deviation has occurred is shown as the following
Fig. 2.4.
Fig. 2.4 The integral action with constant deviation
4) The expression of I action is as following;
As shown in the expression, Integral action can be made stronger or weaker by
adjusting integration time (K
i
) in I action.
That is, the more the integration time (the longer the integration time) as shown in
Fig. 2.5, the lesser the quantity added to or subtracted from the MV and the longer
the time needed for the PV to reach the SV.
As shown in Fig. 2.6, when the integration time given is short the PV will approach
the SV in short time since the quantity added or subtracted become increased. But,
If the integration time is too short then oscillations occur, therefore, the proper P
and I value is requested.
∫
=
Edt
Ti
Kp
MV