Chapter 15. The PID functions
15-14
15.2.2.3
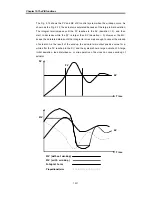
D control
The continuous formula of derivative term is as following;
dt
dy
KTd
D
D
dt
d
N
Td
−
=
+
×
N : high frequency noise depression ration
y : the object to be controlled (PV)
The digitized formula is as following (Use Tustin approximation method)
[
]
)
1
(
)
(
2
2
)
1
(
2
2
)
(
−
−
+
−
−
+
−
=
n
y
n
y
hN
Td
KTdN
n
D
hN
Td
hN
Td
n
D
15.2.2.4
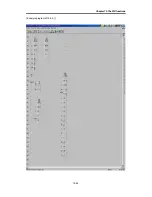
Pseudo code of PID control
The pseudo code of PID control is as following;
Step 1 : Get constants that are used for PID operation
Ti
h
K
Bi
×
=
: integral gain
)
2
(
)
2
(
h
N
Td
h
N
Td
Ad
×
+
×
×
−
×
=
: derivation gain
)
2
(
)
2
(
h
N
Td
Td
N
K
Bd
×
+
×
×
×
×
=
Tt
h
A
=
0
: anti-windup gain
Step 2 : Read SV and PV value
PV = adin(ch1)
Step 3: Calculate the proportional term.
P = K
×
(b
×
SV – PV)
Step 4 : Update the derivative term. (initial value of D = 0)
D = As
×
D – Bd
×
(PV – PV_old)
Step 5 : Calculate the MV. (initial value of I = 0)
MV = P + I + D
Step 6 : Check the actuator is saturated or not.
U = sat(MV, U_low, U_high)
Step 7 : Output the MV value to the D/A module
Step 8 : Update the integral term.
I = I + bi
×
(SV – PV) + A0
×
(U – MV)
Step 9 : Update the PV_old value.
PV_old = PV