MOTOROLA
DSP96002 USER’S MANUAL
C-13
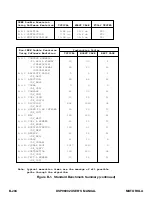
source is moved to the 52 bit fraction of the destination, and the implicit integer bit is made explicit. If the
number is denormalized, the V tag is set. Again, extra cycles may be required when a denormalized number
is used as an operand, depending on the FZ bit in the SR. The 11-bit exponent of the source is copied to
the 11-bit exponent of the destination.
When moving DP numbers from the data ALU to memory, the above process is reversed, as shown in Fig-
ure C-10b. Note that the 52-bit fraction may actually consist of 21 zeros if the number in question was the
result of a SEP arithmetic or 29 zeros in the case of a SP move. SEP arithmetic result precision can only
be retained in memory by using DP moves.
C.1.5.1.1
FLOATING-POINT MOVES TO/FROM DATA ALU REGISTERS
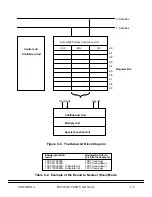
The following sections deal with the case where a write (move in) is followed by a read (move out) without
any floating-point operation being actually performed on the Data ALU register (save-restore procedure).
The only way to provide correct results for save-restore procedures is to perform the same type of moves
when writing and then reading the register (SP write followed by SP read or DP write followed by DP read).
C.1.5.1.1.1
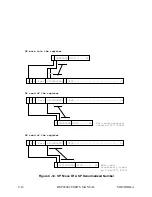
Single Precision (SP) Move Of A SP Normalized Number
This section illustrates what happens when a 32-bit source (normalized single precision) is written by a sin-
gle precision floating-point move and the data is stored in a Data ALU floating-point register D0-D9. Fol-
lowing the above operation, the Data ALU register will be read first by a single precision and then by a dou-
ble precision floating-point move.
- 32-bit data from source is 3F800000 (= +1.0)
- exp = 7F (8 bit bias)
- mantissa = 000000 (the hidden bit is one)
- data stored in the register
- e = 3FF (correct representation with 11-bit bias)
- I = 1 (the number is normalized so hidden bit is 1)
- U-TAG = 0 (cleared; the number can be used in computations
without adding extra cycles for normalization,
since it is a normalized number)
- fraction = 00...00 - mantissa = 1.00...00
One should notice that both single and double precision floating-point moves out of the register will produce
correct results in this case as shown in Figure C-11.
Summary of Contents for DSP96002
Page 3: ...1 2 DSP96002 USER S MANUAL MOTOROLA ...
Page 38: ...MOTOROLA DSP96002 USER S MANUAL 3 15 Figure 3 4 Modulo Arithmetic Unit Block Diagram ...
Page 39: ...3 16 DSP96002 USER S MANUAL MOTOROLA ...
Page 53: ...4 14 DSP96002 USER S MANUAL MOTOROLA ...
Page 76: ...MOTOROLA DSP96002 USER S MANUAL 5 23 Figure 5 8 Address Modifier Summary ...
Page 86: ...6 10 DSP96002 USER S MANUAL MOTOROLA ...
Page 101: ...MOTOROLA DSP96002 USER S MANUAL 7 15 Figure 7 9 HI Block Diagram One Port ...
Page 140: ...7 54 DSP96002 USER S MANUAL MOTOROLA ...
Page 166: ...9 10 DSP96002 USER S MANUAL MOTOROLA ...
Page 181: ...MOTOROLA DSP96002 USER S MANUAL 10 15 Figure 10 8 Program Address Bus FIFO ...
Page 337: ...MOTOROLA DSP96002 USER S MANUAL A 149 ...
Page 404: ...A 216 DSP96002 USER S MANUAL MOTOROLA PC xxxx D ...
Page 460: ...A 272 DSP96002 USER S MANUAL MOTOROLA SIOP Not affected ...
Page 484: ...A 296 DSP96002 USER S MANUAL MOTOROLA SSH PC SSL SR SP 1 SP ...
Page 519: ...MOTOROLA DSP96002 USER S MANUAL A 331 ...
Page 718: ...MOTOROLA DSP96002 USER S MANUAL B 199 ...
Page 871: ... MOTOROLA INC 1994 MOTOROLA TECHNICAL DATA SEMICONDUCTOR M Addendum ...
Page 888: ...MOTOROLA INDEX 1 INDEX ...
Page 889: ......