4.15
EDH0162En1040 – 06/99
MM4005
Motion Control Tutorial
The result is that the integral term will increase until it drives the motor by
itself, reducing the following error to zero. At stop, this has the very desir-
able effect of driving the positioning error to zero. During a long constant-
velocity motion it also brings the following error to zero, an important
feature for some applications.
Unfortunately, the integral term also has a negative side, a severe de-stabi-
lizing effect on the servo loop. In the real world, a simple PI loop is usually
undesirable.
4.3.1.3
PID Loop
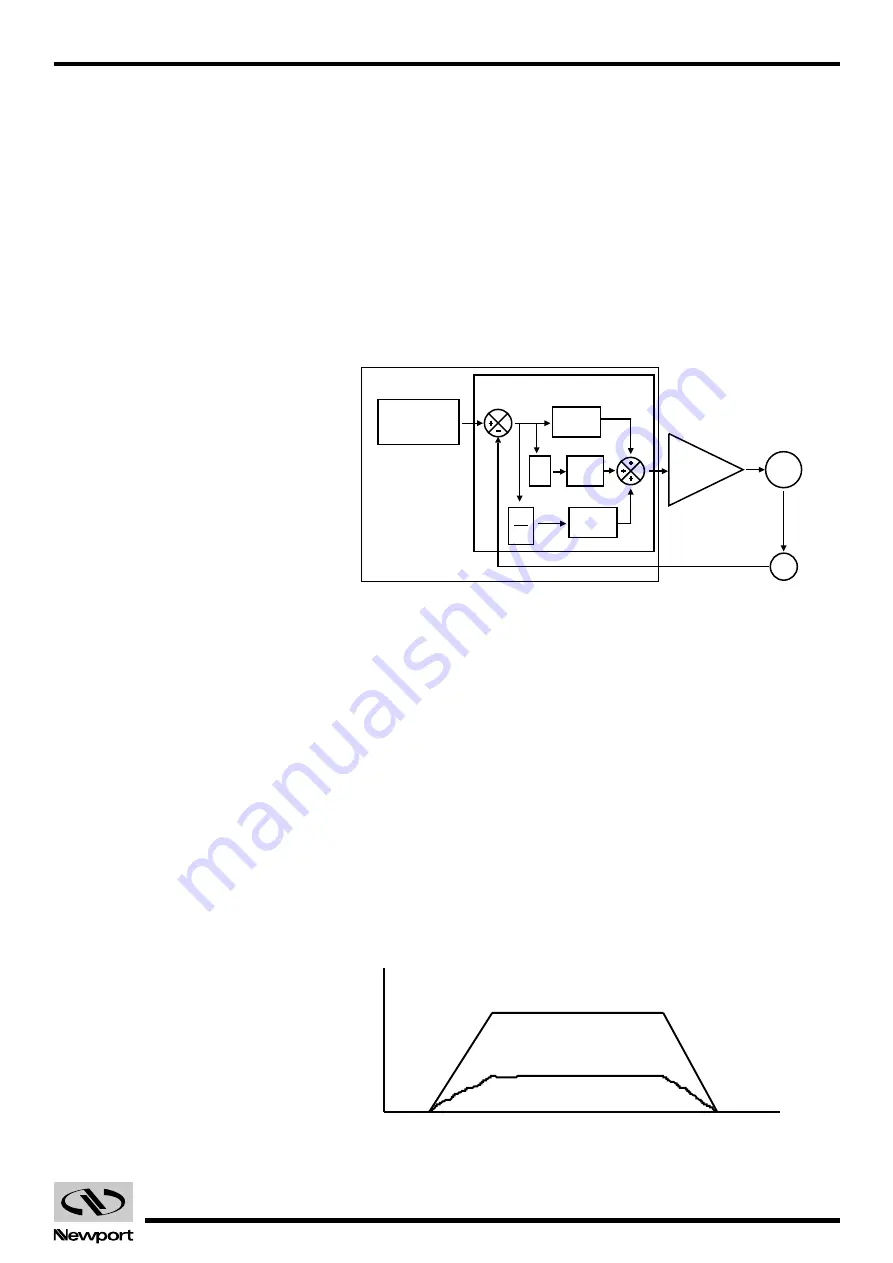
The third term of the PID loop is the derivative term. It is defined as the dif-
ference between the following error of the current servo cycle and of the pre-
vious one. If the following error does not change, the derivative term is zero.
Fig. 4.16
— PID Loop.
Fig. 4.16 shows the PID servo loop diagram. The derivative term is added to
the proportional and integral one. All three process the following error in
their own way and, added together, form the control signal.
The derivative term adds a damping effect which prevents oscillations and
position overshoot.
4.3.2
Feed-Forward Loops
As described in the previous paragraph, the main driving force in a PID
loop is the proportional term. The other two correct static and dynamic
errors associated with the closed loop.
Taking a closer look at the desired and actual motion parameters and at the
characteristics of the DC motors, some interesting observations can be
made. For a constant load, the velocity of a DC motor is approximately pro-
portional with the voltage. This means that for a trapezoidal velocity profile,
for instance, the motor voltage will have also a trapezoidal shape (Fig. 4.17).
Fig. 4.17
— Trapezoidal Velocity Profile.
Time
Desired Velocity
Motor Voltage
X
K
p
X
K
i
X
K
d
de
dt
e
Trajectory
Generator
Motion Controller
Servo Controller
Driver
Motor
Encoder
∫
e
Artisan Technology Group - Quality Instrumentation ... Guaranteed | (888) 88-SOURCE | www.artisantg.com