85
DE
14
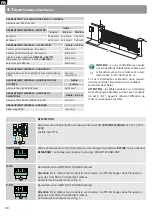
ŝĂŐŶŽƐƟŬͲĞƚƌŝĞďƐĂƌƚ/ŶĨŽ
TEST
x5 s
TEST
1 click
...
PER USCIRE
DALLA MODALITA’
/ŶĚĞƌĞƚƌŝĞďƐĂƌƚ/E&KǁĞƌĚĞŶĞŝŶŝŐĞDĞƐƐǁĞƌƚĞĚĞƌ^ƚĞƵĞƌƵŶŐ
B70/2DC
angezeigt.
/Ŷ ĚĞƌ ĞƚƌŝĞďƐĂƌƚ ͣĞĚŝĞŶĞůĞŵĞŶƚĞ ƵŶĚ ^ŝĐŚĞƌŚĞŝƚƐǀŽƌƌŝĐŚƚƵŶŐĞŶ ĂŶnjĞŝŐĞŶ͞ ƵŶĚ ďĞŝ ĂƵƐŐĞƐĐŚĂůƚĞƚĞŵ DŽƚŽƌ͕ ĚŝĞ
dĂƐƚĞ d^d ϱ ^ĞŬƵŶĚĞŶ ůĂŶŐ ŐĞĚƌƺĐŬƚ ŚĂůƚĞŶ͘ ĂƐ ^ƚĞƵĞƌŐĞƌćƚ njĞŝŐƚ ŶĂĐŚĞŝŶĂŶĚĞƌ ĚŝĞ ĨŽůŐĞŶĚĞŶ WĂƌĂŵĞƚĞƌ ƵŶĚ ĚĞŶ
ĞŶƚƐƉƌĞĐŚĞŶĚĞŶĞƌĨĂƐƐƚĞŶtĞƌƚĂŶ͗
Parameter
&ƵŶŬƟŽŶ
&QW
&QW
ĞŝŐƚĚŝĞWŽƐŝƟŽŶ͕ŝŶĚĞƌƐŝĐŚĚĞƌDKdKZϭͬDKdKZϮďĞĮŶĚĞƚ͕ĂƵƐŐĞĚƌƺĐŬƚŝŶhŵĚƌĞŚƵŶŐĞŶnjƵŵĞŝƚƉƵŶŬƚĚĞƌ
WƌƺĨƵŶŐŝŵsĞƌŐůĞŝĐŚnjƵƌ'ĞƐĂŵƚůćŶŐĞ͘
/ Q
/ Q
ŶnjĞŝŐĞĚĞƌ'ĞƐĂŵƚůćŶŐĞĚĞƐƉƌŽŐƌĂŵŵŝĞƌƚĞŶĚĞƐDKdKZ^ϭͬDKdKZ^Ϯ,ƵďƐŝŶhŵĚƌĞŚƵŶŐĞŶ͘
U3
U3
ŶnjĞŝŐĞĚĞƌDŽƚŽƌŐĞƐĐŚǁŝŶĚŝŐŬĞŝƚĚĞƐDKdKZ^ϭͬDKdKZ^ϮŝŶhŵĚƌĞŚƵŶŐĞŶƉƌŽDŝŶƵƚĞ͘
$ 3
$ 3
ŶnjĞŝŐĞĚĞƌDŽƚŽƌƐƚƌŽŵĂƵĨŶĂŚŵĞĚĞƐDKdKZ^ϭͬDKdKZ^ϮŝŶŵƉĞƌĞ;ĞŝƐƉŝĞů͗ϬϬϭ͘ϭсϭ͕ϭ͘͘͘͘Ϭϭϲ͘ϱсϭϲ͕ϱͿ͘
ĞŝƐƟůůƐƚĞŚĞŶĚĞŵDŽƚŽƌŝƐƚĚŝĞ^ƚƌŽŵĂƵĨŶĂŚŵĞŐůĞŝĐŚϬ͘/ŶĚĞŵŵĂŶĞŝŶĞŶĞĨĞŚůĞƌƚĞŝůƚ͕ŬĂŶŶŵĂŶĚĞŶĂƵĨŐĞŶŽŵ
-
ŵĞŶĞŶ^ƚƌŽŵĞƌĨĂƐƐĞŶ͘
E86
ŶnjĞŝŐĞĚĞƐŽƌĚŶƵŶŐƐŐĞŵćƘĞŶŶůĂŐĞŶnjƵƐƚĂŶĚƐ͘ĞŝƐƟůůƐƚĞŚĞŶĚĞŵDŽƚŽƌŬĂŶŶĞŝŶĞŵƂŐůŝĐŚĞmďĞƌůĂƐƚƵŶŐŽĚĞƌ
ĞŝŶĞnjƵŶŝĞĚƌŝŐĞEĞƚnjƐƉĂŶŶƵŶŐĨĞƐƚŐĞƐƚĞůůƚǁĞƌĚĞŶ͘ĐŚƚĞŶ^ŝĞĂƵĨĨŽůŐĞŶĚĞtĞƌƚĞ͗
EĞƚnjƐƉĂŶŶƵŶŐсϮϯϬs;EĞŶŶƐƉĂŶŶƵŶŐͿ͕ďh^с
,
EĞƚnjƐƉĂŶŶƵŶŐсϮϬϳs;ͲϭϬйͿ͕ďh^с
,
EĞƚnjƐƉĂŶŶƵŶŐсϮϱϯs;нϭϬйͿ͕ďh^с
,
& 3
& 3
ĞŝŐƚĚĞŶǀĞƌǁĞŶĚĞƚĞŶ^ƚƌŽŵĂŶ͕ƵŵĞǀĞŶƚƵĞůůĞƌŬĂŶŶƚĞĞĂŶƐƉƌƵĐŚƵŶŐĞŶǀŽŶDKdKZϭͬDKdKZϮnjƵŬŽƌƌŝŐŝĞƌĞŶ͕
ĚŝĞďĞŝƐƉŝĞůƐǁĞŝƐĞĂƵĨĚŝĞŶŝĞĚƌŝŐĞƵƘĞŶƚĞŵƉĞƌĂƚƵƌnjƵƌƺĐŬnjƵĨƺŚƌĞŶƐŝŶĚ͕ĂƵƐŐĞĚƌƺĐŬƚŝŶŵƉĞƌĞ;ĞŝƐƉŝĞů͗ϬсϬ
͘͘͘ϰснϯͿ͘Ğŝŵ^ƚĂƌƚĚĞƐdŽƌĂŶƚƌŝĞďƐǀŽŶŐĂŶnjŽīĞŶŽĚĞƌŐĂŶnjŐĞƐĐŚůŽƐƐĞŶĞƌŚƂŚƚĚĂƐ^ƚĞƵĞƌŐĞƌćƚ͕ǁĞŶŶĞƐĞŝŶĞ
ƐƚćƌŬĞƌĞĞĂŶƐƉƌƵĐŚƵŶŐĨĞƐƚƐƚĞůůƚ͕ĂůƐďĞŝŵŝŶůĞƌŶĞŶĚĞƐdŽƌůĂƵĨƐŐĞƐƉĞŝĐŚĞƌƚ͕ĂƵƚŽŵĂƟƐĐŚĚĞŶĂŶĚĞŶDKdKZϭͬ
DKdKZϮĂďnjƵŐĞďĞŶĚĞŶ^ƚƌŽŵ͘
$6&
$6&
ĞŝŐƚ ĚŝĞ ^ĐŚǁĞůůĞ ĚĞƐ ^ƚƌŽŵƐ ĂŶ͕ ďĞŝ ĚĞƌ ĚŝĞ ,ŝŶĚĞƌŶŝƐĞƌŬĞŶŶƵŶŐ ;YƵĞƚƐĐŚƐĐŚƵƚnjͿ ĚĞƐ DKdKZ^ ϭ ͬ DKdKZ^ Ϯ
ĂƵƐŐĞůƂƐƚǁŝƌĚ͕ĂƵƐŐĞĚƌƺĐŬƚŝŶŵƉĞƌĞ͘ĞƌtĞƌƚǁŝƌĚĂƵƚŽŵĂƟƐĐŚǀŽŵ^ƚĞƵĞƌŐĞƌćƚĂƵĨĚĞƌ'ƌƵŶĚůĂŐĞĚĞƌŝŶƐƚĞů
-
lungen der Parameter
,
und
ďĞƌĞĐŚŶĞƚ͘
&ƺƌĞŝŶĞŶŬŽƌƌĞŬƚĞŶĞƚƌŝĞďĚĞƐDŽƚŽƌƐŵƵƐƐ
$ 3
immer niedriger sein als der Wert
$6&
.
7,Q
7,Q
ŶnjĞŝŐĞĚĞƐĞŝƚƌĂƵŵƐŝŶ^ĞŬƵŶĚĞŶ͕ĚĞŶĚĞƌDŽƚŽƌũĞŶĂĐŚŝŶƐƚĞůůƵŶŐĚĞƐWĂƌĂŵĞƚĞƌƐďĞŶƂƟŐƚ͕ƵŵĞŝŶ,ŝŶĚĞƌŶŝƐ
njƵĞƌŬĞŶŶĞŶ
/
.
Beispiel
.
= 1 s /
.
сϬ͕ϭϮƐ;ϭϮϬŵƐͿ͘^ŝĐŚĞƌƐƚĞůůĞŶ͕ĚĂƐƐĚŝĞDŽƚŽƌůĂƵĨnjĞŝƚƺďĞƌϬ͕ϯƐďĞƚƌćŐƚ͘
D%V
D%6
ŶnjĞŝŐĞĨƺƌĚĞŶŐƵƚĞŶƵƐƚĂŶĚĚĞƐDKdKZ^ϭͬDKdKZ^Ϯ͘hŶƚĞƌŶŽƌŵĂůĞŶĞĚŝŶŐƵŶŐĞŶŝƐƚĚĞƌtĞƌƚŐĞƌŝŶŐĞƌĂůƐϱϬϬ͘
tĞŶŶĚĞƌtĞƌƚŚƂŚĞƌŝƐƚĂůƐϮϬϬϬďůŽĐŬŝĞƌƚĚĂƐ^ƚĞƵĞƌŐĞƌćƚĚĞŶDŽƚŽƌ͘ŝŶtĞƌƚƺďĞƌϱϬϬnjĞŝŐƚĂŶ͕ĚĂƐƐĚŝĞYƵĂůŝƚćƚ
ĚĞƐsĞƌďŝŶĚƵŶŐƐŬĂďĞůƐŶŝĐŚƚĨƺƌĚŝĞ/ŶƐƚĂůůĂƟŽŶŐĞĞŝŐŶĞƚŝƐƚ͗ĚĂƐsĞƌďŝŶĚƵŶŐƐŬĂďĞůŝƐƚnjƵůĂŶŐŽĚĞƌƐĞŝŶYƵĞƌƐĐŚŶŝƩŝƐƚ
ŶŝĐŚƚŐĞĞŝŐŶĞƚŽĚĞƌĞƐůŝĞŐƚĞŝŶĞůĞŬƚƌŝƐĐŚĞƐWƌŽďůĞŵĂŵƌƵƐŚůĞƐƐͲDŽƚŽƌǀŽƌ͘
83
tĞŶŶĚĂƐ^ƚĞƵĞƌŐĞƌćƚĚŝĞWŽƐŝƟŽŶĚĞƌdŽƌŇƺŐĞůnjƵŵĞŝƚƉƵŶŬƚĚĞƌWƌƺĨƵŶŐŬĞŶŶƚ͕njĞŝŐƚĚĂƐŝƐƉůĂLJĂŶ͗
83
BB
WŽƐŝƟŽŶďĞŬĂŶŶƚ͕ŶŽƌŵĂůĞƌĞƚƌŝĞď͘
83
B
WŽƐŝƟŽŶĚĞƐ&>m'>^ϭŶŝĐŚƚďĞŬĂŶŶƚ͕WŚĂƐĞnjƵƌ<ŽƌƌĞŬƚƵƌĚĞƌWŽƐŝƟŽŶůćƵŌ͘
83
B
WŽƐŝƟŽŶĚĞƐ&>m'>^ϮŶŝĐŚƚďĞŬĂŶŶƚ͕WŚĂƐĞnjƵƌ<ŽƌƌĞŬƚƵƌĚĞƌWŽƐŝƟŽŶůćƵŌ͘
83
WŽƐŝƟŽŶďĞŝĚĞƌ&ůƺŐĞůŶŝĐŚƚďĞŬĂŶŶƚ͕WŚĂƐĞnjƵƌ<ŽƌƌĞŬƚƵƌĚĞƌWŽƐŝƟŽŶůćƵŌ͘
2&
ƵƐƚĂŶĚƐĂŶnjĞŝŐĞĚĞƐŶƚƌŝĞďƐ;ŽīĞŶͬŐĞƐĐŚůŽƐƐĞŶͿ͘
2&23
ŶƚƌŝĞďŝŶĚĞƌPīŶƵŶŐƐƉŚĂƐĞ;DŽƚŽƌĂŬƟǀͿ͘
23&/
ŶƚƌŝĞďŝŶ^ĐŚůŝĞƘƵŶŐƐƉŚĂƐĞ;DŽƚŽƌĂŬƟǀͿ͘
2S
2
ŶƚƌŝĞďǀŽůůƐƚćŶĚŝŐŐĞƂīŶĞƚ;DŽƚŽƌŶŝĐŚƚĂŬƟǀͿ͘
2S
&
ŶƚƌŝĞďǀŽůůƐƚćŶĚŝŐŐĞƐĐŚůŽƐƐĞŶ;DŽƚŽƌŶŝĐŚƚĂŬƟǀͿ͘
8)
8)8
B
EĞƚnjƐƉĂŶŶƵŶŐnjƵŶŝĞĚƌŝŐŽĚĞƌƺďĞƌůĂƐƚĞƚ͘
8)
B
+
mďĞƌƐƚƌŽŵĂŵtĞĐŚƐĞůƌŝĐŚƚĞƌ͘
ͻ tĞŶŶŶƵƌĞŝŶDŽƚŽƌĂŵ^ƚĞƵĞƌŐĞƌćƚĂŶŐĞƐĐŚůŽƐƐĞŶŝƐƚ͕ǁĞƌĚĞŶŶƵƌĚŝĞWĂƌĂŵĞƚĞƌnjƵŵ͞DKdKZϭ͟ĂŶŐĞnjĞŝŐƚ͘
ͻ hŵnjǁŝƐĐŚĞŶĚĞŶĞŝŶnjĞůŶĞŶWĂƌĂŵĞƚĞƌŶnjƵǁĞĐŚƐĞůŶ͕ĚŝĞdĂƐƚĞŶнͬͲǀĞƌǁĞŶĚĞŶ͘ĞŝŵƌƌĞŝĐŚĞŶĚĞƐůĞƚnjƚĞŶWĂƌĂŵĞƚĞƌƐ
ĚŝĞdĂƐƚĞͲďĞƚćƟŐĞŶ͕ƵŵǁŝĞĚĞƌnjƵƌƺĐŬnjƵŬĞŚƌĞŶ͘
ͻ /ŶĚĞƌĞƚƌŝĞďƐĂƌƚ/E&KŬĂŶŶĚĞƌŶƚƌŝĞďďĞƚćƟŐƚǁĞƌĚĞŶ͕ƵŵƐĞŝŶĞ&ƵŶŬƟŽŶŝŶĐŚƚnjĞŝƚnjƵƉƌƺĨĞŶ͘
ͻ hŵĚŝĞĞƚƌŝĞďƐĂƌƚ/E&KnjƵǀĞƌůĂƐƐĞŶ͕ĚŝĞdĂƐƚĞd^dĞŝŶŝŐĞ^ĞŬƵŶĚĞŶŐĞĚƌƺĐŬƚŚĂůƚĞŶ͘
AUS DER
BESTRIEBSART
h',E