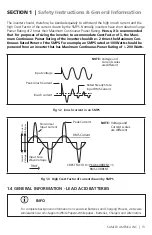
6 | SAMLEX AMErICA INC.
SAMLEX AMErICA INC. | 7
inductive reactance (X
L
), Capacitive reactance (X
C
) and reactance (X):
reactance is the
opposition of a circuit element to a change of electric current or voltage due to that element’s
inductance or capacitance. Inductive reactance (
X
L
) is the property of a coil of wire in resisting
any change of electric current through the coil. It is proportional to frequency and inductance
and causes the current vector to lag the voltage vector by Phase Angle (
φ
) = 90°. Capacitive re-
actance (
X
C
) is the property of capacitive elements to oppose changes in voltage.
X
C
is inversely
proportional to the frequency and capacitance and causes the current vector to lead the voltage
vector by Phase Angle (
φ
) = 90°. The unit of both
X
L
and
X
C
is “Ohm” - also denoted as “Ω”.
The effects of inductive reactance
X
L
to cause the current to lag the voltage by 90° and that of
the capacitive reactance
X
C
to cause the current to lead the voltage by 90° are exactly oppo-
site and the net effect is a tendency to cancel each other. Hence, in a circuit containing both
inductances and capacitances, the net
reactance (X)
will be equal to the difference between
the values of the inductive and capacitive reactances. The net
reactance (X)
will be inductive if
X
L
>
X
C
and capacitive if
X
C
>
X
L
.
impedance, Z:
It is the vectorial sum of resistance and reactance vectors in a circuit.
Active Power (P), watts
: It is denoted as “
P
” and the unit is “
watt
”. It is the power that is
consumed in the resistive elements of the load. A load will require additional reactive Power
for powering the inductive and capacitive elements. The effective power required would be the
Apparent Power that is a vectorial sum of the Active and reactive Powers.
reactive Power (Q), VAr:
Is denoted as “
Q
” and the unit is
VAr
. Over a cycle, this power is
alternatively stored and returned by the inductive and capacitive elements of the load. It is not
consumed by the inductive and capacitive elements in the load but a certain value travels from
the AC source to these elements in the (+) half cycle of the sinusoidal voltage (Positive value) and
the same value is returned back to the AC source in the (-) half cycle of the sinusoidal voltage
(Negative value). Hence, when averaged over a span of one cycle, the net value of this power is 0.
However, on an instantaneous basis, this power has to be provided by the AC source.
Hence, the
inverter, AC wiring and over current protection devices have to be sized based on the combined
effect of the Active and Reactive Powers that is called the Apparent Power.
Apparent Power (S), VA:
This power, denoted by “S”, is the vectorial sum of the Active
Power in Watts and the reactive Power in “VAr”. In magnitude, it is equal to the rMS value of
voltage “V” X the rMS value of current “A”. The Unit is VA.
Please note that Apparent Power
VA is more than the Active Power in Watts. Hence, the inverter, AC wiring and over current
protection devices have to be sized based on the Apparent Power.
Maximum Continuous running AC Power rating:
This rating may be specified as “Active
Power” in Watts (W) or “Apparent Power” in Volt Amps (VA). It is normally specified in “Active
Power (P)” in Watts for resistive type of loads that have Power factor =1. reactive types of
loads will draw higher value of “Apparent Power” that is the sum of “Active and reactive
Powers”. Thus, AC power source should be sized based on the higher “Apparent Power”
rating in (VA) for all reactive Types of AC loads. If the AC power source is sized based on the
lower “Active Power” rating in Watts (W), the AC power source may be subjected to overload
conditions when powering reactive Type of loads.
Starting Surge Power rating:
Certain loads require considerably higher Starting Surge Power
for short duration (lasting from tens of millisecs to few seconds) as compared to their Maximum
Continuous running Power rating. Some examples of such loads are given on next page:
SECTIOn 1 |
Safety Instructions & general Information