allowed to do so because, in our approach, the recursive bipartitioning of the target
graph is fully independent with respect to that of the source graph (however, the
opposite is false).
For space and time saving issues, some classical homogeneous architectures (2D
and 3D meshes and tori, hypercubes, complete graphs, etc.) have been algorithmi-
cally coded within the mapper itself by the means of built-in functions. Instead of
containing the whole graph decomposition data, their target files hold only a few
values, used as parameters by the built-in functions.
5.4.1
Decomposition-defined architecture files
Decomposition-defined architecture files are the standard way to describe weighted
and/or irregular target architectures. Several file formats exist, but we only present
here the most humanly readable one, which begins in “
deco 0
” (“
deco
” stands for
“decomposition-defined” architecture, and “
0
” is the format type).
The “
deco 0
” header is followed by two integer numbers, which are the number
of processors and the largest terminal number used in the decomposition, respec-
tively. Two arrays follow. The first array has as many lines as there are processors.
Each of these lines holds three numbers: the processor label, the processor weight
(that is an estimation of its computational power), and its terminal number. The
terminal number associated with every processor is obtained by giving the initial
domain holding all the processors number 1, and by numbering the two subdomains
of a given domain of number
i
with numbers 2
i
and 2
i
+ 1. The second array is
a lower triangular diagonal-less matrix that gives the distance between all pairs of
processors. This distance matrix, combined with the decomposition tree coded by
terminal numbers, allows the evaluation by averaging of the distance between all
pairs of domains. In order for the mapper to behave properly, distances between
processors must be strictly positive numbers. Therefore, null distances are not ac-
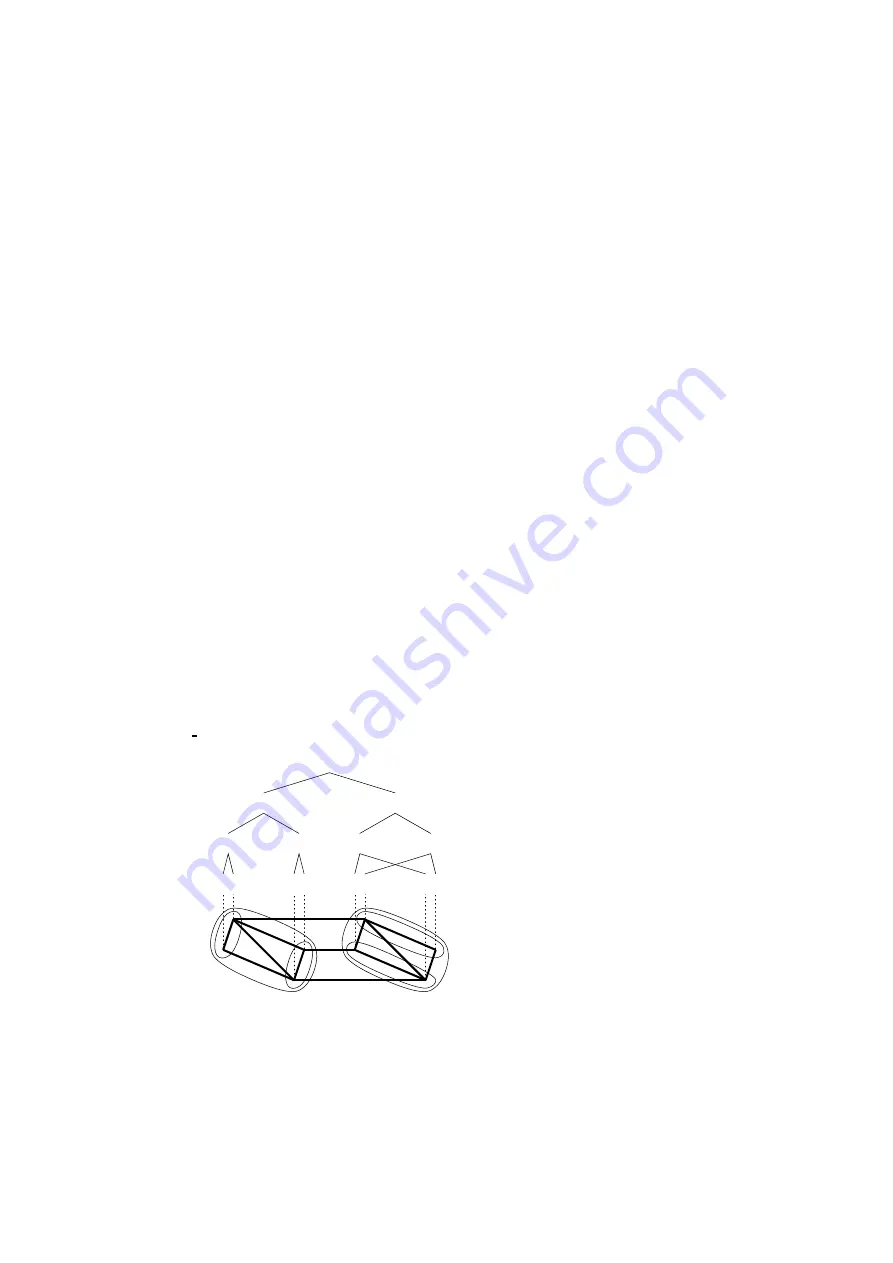
cepted. For instance, Figure 7 shows the contents of the architecture decomposition
file for UB(2
,
3), the binary de Bruijn graph of dimension 3, as computed by the
amk grf
program.
1
7
3
6
12 13
9 11
8 10
5
4
2
14
15
deco 0
8 15
0 1 15
1 1 14
2 1 13
3 1 11
4 1 12
5 1 9
6 1 8
7 1 10
1
2 1
2 1 2
1 1 1 2
3 2 1 1 2
2 2 2 1 1 1
3 2 3 1 2 2 1
Figure 7: Target decomposition file for UB(2
,
3). The terminal numbers associated
with every processor define a unique recursive bipartitioning of the target graph.
23
















































