123
Appendix
Equations that are difficult to solve
Newton’s method has problems in solving
certain types of equations, either because
the tangential lines it uses to approximate the
solutions iterate only slowly toward the
correct answer, or because they do not
iterate there at all. Examples of such
equations include equations of which steep
slopes are a feature (e.g.
y
= 10
x
–5), periodic
functions (e.g.
y
= sin
x
), functions featuring
an inflection (e.g.
y
=
x
3
–3
x
2
+
x
+ 5) and
functions where the unknown variable
appears as a denominator (e.g.
y
= 8/
x
+ 1).
Many of those equations may become
soluble if a range of expected values is
defined that corresponds closely to the real
solution.
• For periodic functions such as sin
x
and
cos
x
, the gradient near peaks or
troughs is very shallow. If the initial
expected value falls too close to a peak
or trough, the calculator may iterate to
a totally different cycle of the function
and will not obtain an accurate solution.
Make sure the initial expected value is
an appropriate distance between a
peak and a trough.
• Where appropriate, you can try
rearranging the equation so that the
unknown variable is no longer a
denominator.
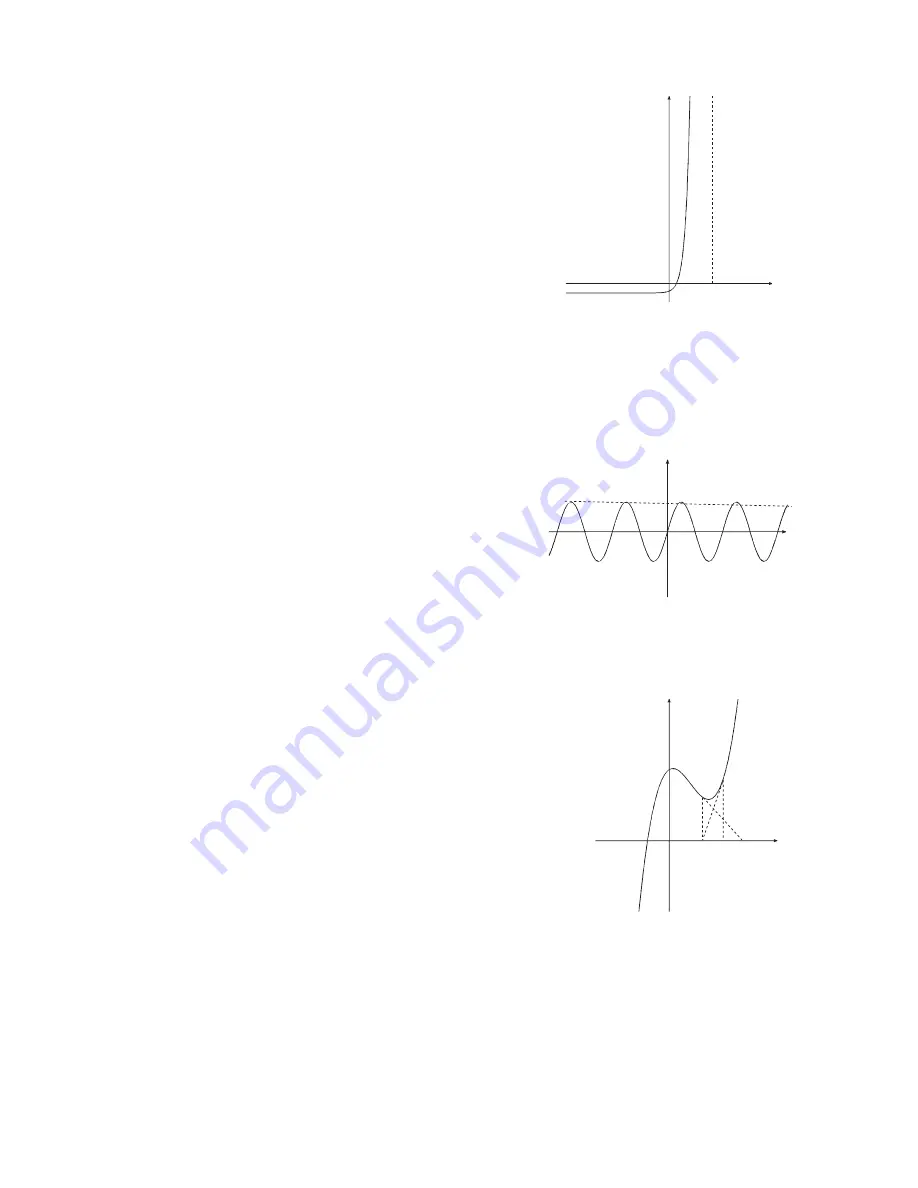
Solving
y
=10
x
– 5 for
y
= 0.
Because of the steep slope, it
takes a long time to iterate to the
correct solution. Set limits a and
b as close as possible either side
of your expected solution.
y
x
Solving
y
= sin
x
for
y
= 0.
If the Initial expected value is too
close to a peak, the calculator
will iterate away from the correct
solution.
Solving
y
=
x
3
– 3
x
2
+
x
+ 5 for
y
= 0.
If the initial expected value is
x
= 3, no solution is obtained.
However, setting
x
to –3 gives
the correct solution of –1.
y
x
Summary of Contents for EL-5230
Page 1: ...PROGRAMMABLE SCIENTIFIC CALCULATOR OPERATION MANUAL EL 5230 EL 5250 ...
Page 2: ......
Page 12: ...10 ...
Page 62: ...60 ...
Page 132: ......








































