50
High school
Fibonacci
• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •
Introduce the sequence to the students and give them the opportunity to try to generate it on
their calculators. After some discussion the students can be shown how to use the temporary
memories to generate the sequence. One method of introducing this is to stick two envelopes
onto the board, one labeled ‘X’ and the other labeled ‘Y’, in which can be placed pieces of paper
marked with the appropriate numbers.
The ratio of successive terms of any such sequence converges to the ‘golden ratio’,
(
1
+
)
÷
2
≈
1
.6
1
803399.
• • • • • • • • • • • • • • • Points for students to discuss • • • • • • • • • • • • • •
Explain orally to students how to generate the Fibonacci sequence on the calculator.
Further Ideas
Ask students for two starting values and then generate the first ten terms of the sequence.
Predict the sum of these of ten numbers, and then ask the students to confirm your answer.
(The ‘trick’ is that the sum of these numbers will always be the sixth number multiplied by
11
.)
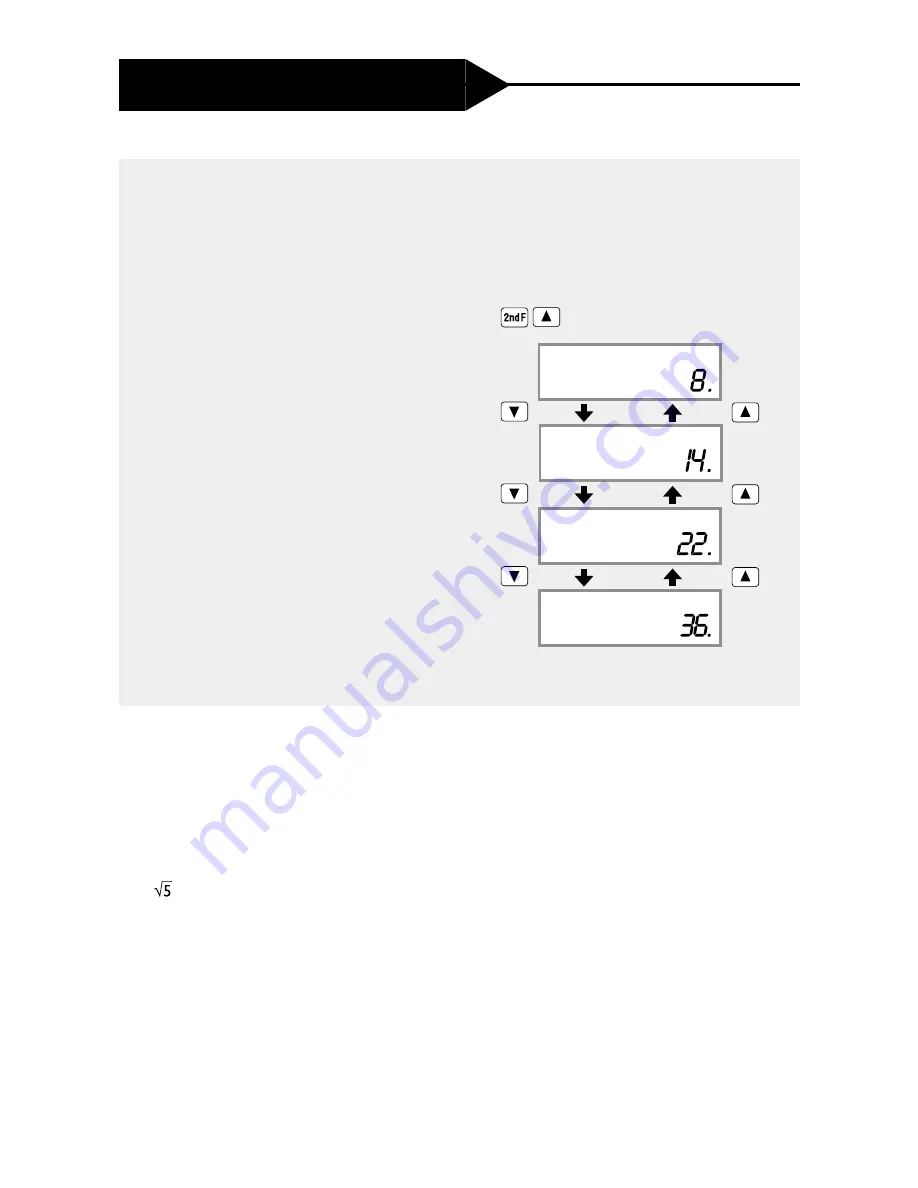
[2, 6, 8,
1
4, 22, ?…]
Find additional members of the series by repeating the above operation.
[2, 6, 8,
1
4, 22, 36, 58…]
This yields the series:
Recall the first formula
Try generating similar series using a variety
of other numbers.
For each of your sequences, once you have
generated a large number of terms, divide
the last term by the preceding term and
note the answer.
......
2+6=
DEG
6+8
DEG
8+14
DEG
14+22
DEG
Summary of Contents for EL-531RH
Page 1: ...SCIENTIFIC CALCULATOR TEACHER S GUIDE JULY 1999 EL 531RH ...
Page 56: ......





































