EL-9600/9400 Graphing Calculator
2-2
There may be differences in the results of calculations and graph plotting depending on the setting.
Return all settings to the default value or to delete all data.
Before
Start
Notes
Step & Key Operation
(When using EL-9600)
*Use either pen touch or cursor to operate.
Display
(When using EL-9600)
Shifting a Graph of Quadratic Equations
A quadratic equation of
y
in terms of
x
can be expressed by the standard form
y = a
(
x -
h
)
2
+ k,
where
a
is the coefficient of the second degree term (
y = ax
2
+ bx + c
) and (
h
, k
) is the vertex
of the parabola formed by the quadratic equation. An equation where the largest exponent
on the independent variable
x
is 2 is considered a quadratic equation. In graphing quadratic
equations on the calculator, let the
x-
variable be represented by the horizontal axis and let
y
be represented by the vertical axis. The relation of an equation and its graph can be seen by
moving the graph and checking the coefficients of the equation.
○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
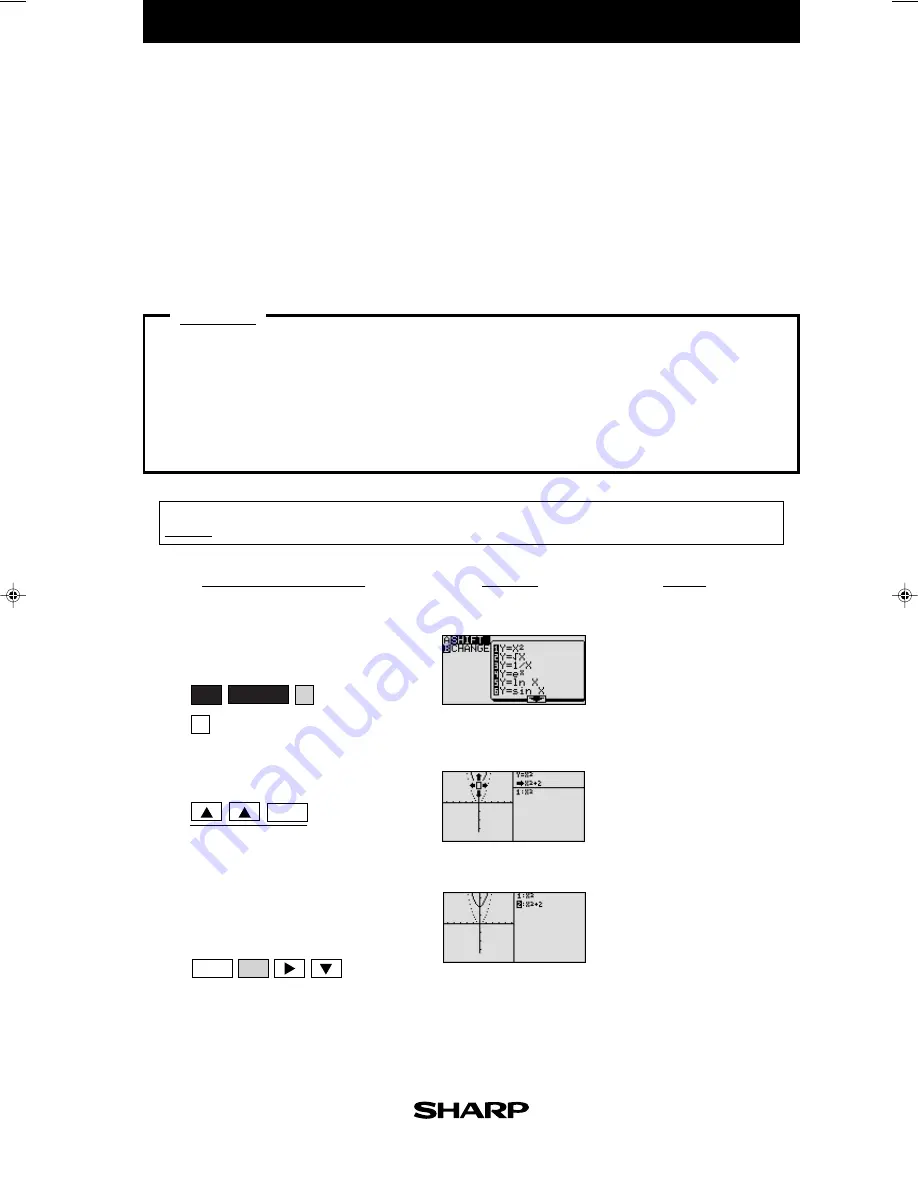
Move or pinch a graph of quadratic equation
y = x
2
to verify the relation between
the coefficients of the equation and the graph.
Example
1.
Shift the graph
y = x
2
upward by 2.
2.
Shift the graph
y = x
2
to the right by 3.
3.
Pinch the slope of the graph
y = x
2
.
1
-
1
Access Shift feature and select the
equation
y = x
2
.
*
*
1
-
2
Move the graph
y = x
2
upward by 2.
*
Save the new graph and observe the
changes in the graph and the
equation.
1
-
3
Notice that upward movement
of the basic
y =
x
2
graph by 2
units in the direction of the
y-
axis means addition of 2 to the
y-
intercept. This demonstrates
that upward movement of the graph by
k
units means
adding a
k
(>0) in the standard form
y = a
(
x -
h
)
2
+ k.
1
2nd F SHIFT/CHANGE
A
ENTER
ENTER
ALPHA
HB1.DocA.
98.10.1, 10:29 AM
8





































