EL-9600/9400 Graphing Calculator
Parallel and Perpendicular Lines
1-2
1.
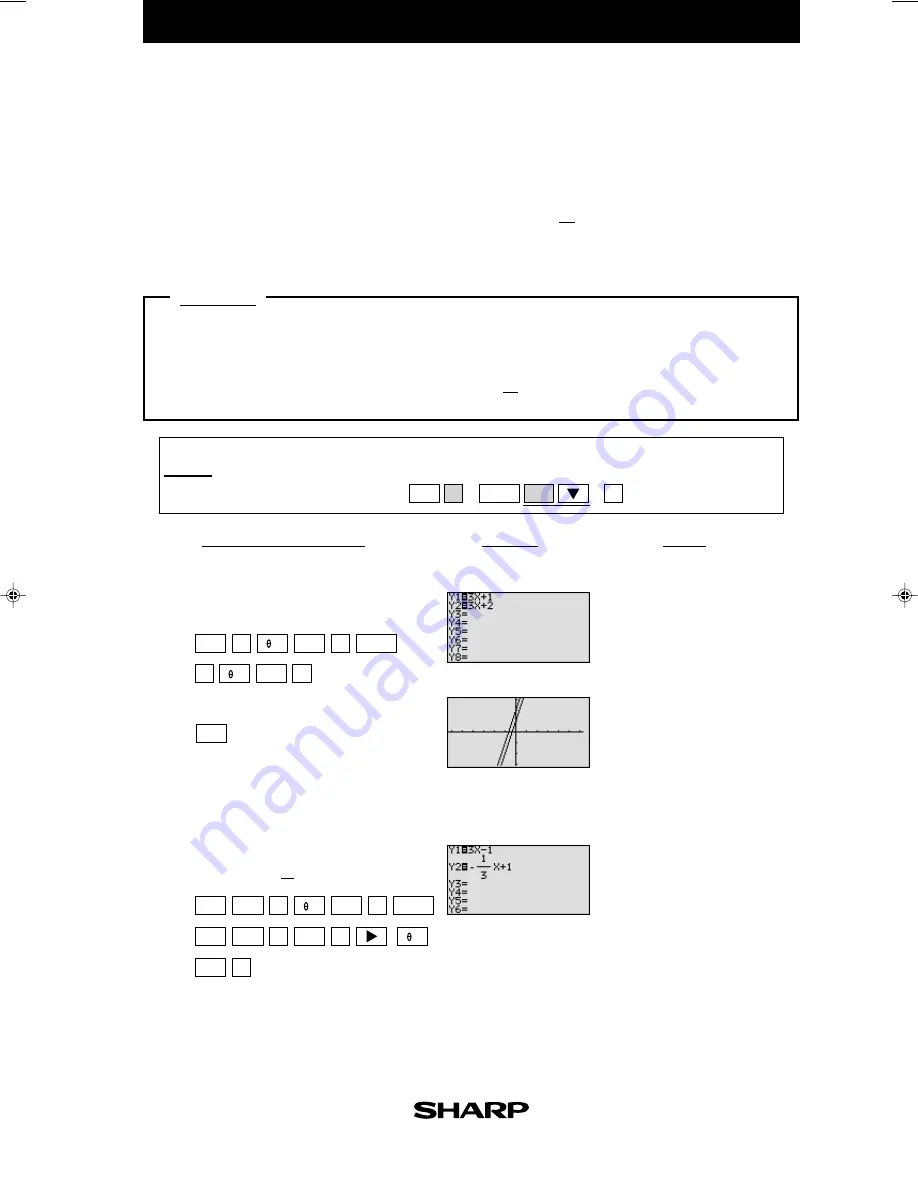
Graph the equations
y =
3
x +
1 and
y =
3
x +
2.
2.
Graph the equations
y =
3
x -
1 and
y = - x +
1
.
Enter the equations
y =
3
x +
1 for
Y1 and
y =
3
x +
2 for Y2.
View the graphs.
1
-
1
Graph parallel lines and perpendicular lines.
1
-
2
Example
○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
Enter the equations
y =
3
x -
1 for
Y1 and
y = - x +
1
for
Y2
.
2
-
1
These lines have an equal
slope but different
y
- inter-
cepts. They are called paral-
lel, and will not intersect.
1
3
*
*
*
1
3
Parallel and perpendicular lines can be drawn by changing the slope of the linear equation
and the
y
intercept. A linear equation of
y
in terms of
x
can be expressed by the slope-
intercept form
y = mx + b
, where
m
is the slope and
b
is the
y
-intercept.
Parallel lines have an equal slope with different
y-
intercepts. Perpendicular lines have
slopes that are negative reciprocals of each other (
m = - ).
These characteristics can be
verified by graphing these lines.
Notes
Step & Key Operation
(When using EL-9600)
*Use either pen touch or cursor to operate.
Display
(When using EL-9600)
There may be differences in the results of calculations and graph plotting depending on the setting.
Return all settings to the default value or to delete all data.
Set the zoom to the decimal window:
*
(
*
)
*
Before
Start
1
m
Y=
ZOOM
C
ENTER
ALPHA
7
3
+
1
ENTER
3
2
+
GRAPH
Y=
CL
3
1
1
1
3
—
(
-
)
CL
ENTER
+
a/b
X
/
/
T
/
n
X
/
/
T
/
n
X
/
/
T
/
n
X
/
/
T
/
n
HB1.DocA.
98.10.1, 10:28 AM
4








































