EL-9600 Graphing Calculator
Slope and Intercept of Quadratic Equations
A quadratic equation of
y
in terms of
x
can be expressed by the standard form
y = a
(
x -
h
)
2
+ k,
where
a
is the coefficient of the second degree term (
y = ax
2
+ bx + c
) and (
h
, k
) is the
vertex of the parabola formed by the quadratic equation. An equation where the largest
exponent on the independent variable
x
is 2 is considered a quadratic equation. In graphing
quadratic equations on the calculator, let the
x-
variable be represented by the horizontal
axis and let
y
be represented by the vertical axis. The graph can be adjusted by varying the
coefficients
a,
h
,
and
k.
2-1
There may be differences in the results of calculations and graph plotting depending on the setting.
Return all settings to the default value or to delete all data.
As Substitution feature is only available on the EL-9600, this section does not apply to the EL-9400.
Before
Start
Graph various quadratic equations and check the relation between the graphs and
the values of coefficients of the equations.
Example
1.
Graph
y = x
2
and
y =
(
x -
2)
2
.
2.
Graph
y = x
2
and
y = x
2
+
2
.
3.
Graph
y = x
2
and
y =
2
x
2
.
4.
Graph
y = x
2
and
y = -
2
x
2
.
1
-
1
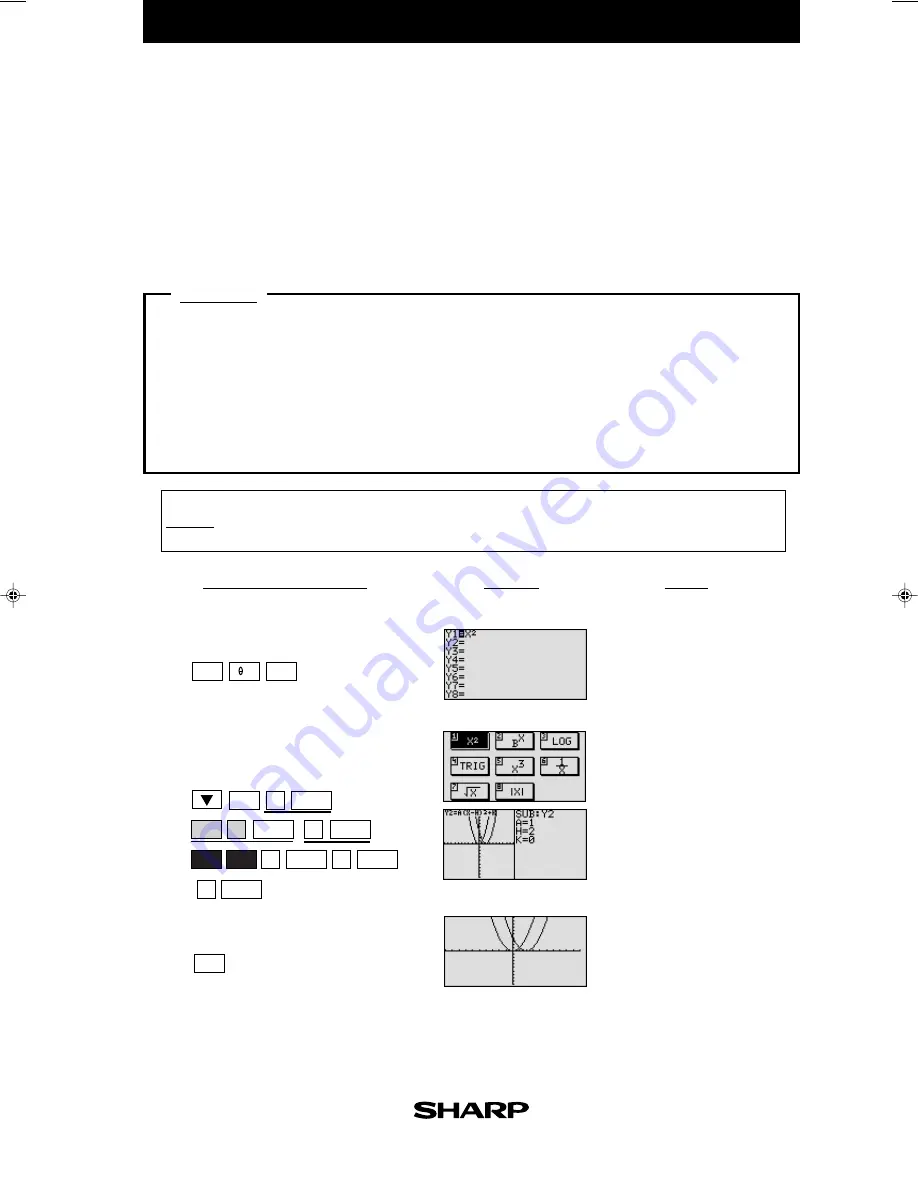
Enter the equation y = x
2
for Y1.
Notes
Step & Key Operation
*Use either pen touch or cursor to operate.
Display
1
-
2
Enter the equation y = (x - 2)
2
for
Y2 using Sub feature.
*
*
*
(
)
○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
Notice that the addition of -2
within the quadratic operation
moves the basic
y
=
x
2
graph
right two units (adding 2 moves
it left two units) on the
x
-axis.
This shows that placing an
h
(>0) within the standard
form
y
=
a
(
x -
h
)
2
+
k
will move the basic graph right
h
units and placing an
h
(<0) will move it left
h
units
on the
x
-axis.
View both graphs.
1
-
3
ENTER
Y=
x
2
EZ
1
1
2
1
0
ENTER
ENTER
ENTER
ENTER
GRAPH
ENTER
ALPHA
C
2nd F
SUB
X
/
/
T
/
n
HB1.DocA.
98.10.1, 10:29 AM
6









































