Using Blackline Master 3.2
The following problem appears on
Blackline Master 3.2
. Verify the half angle
formula cos = ± (1 + cos ). To verify the formula, you will graph the “cos
” as Y1 = cos and the “±
” as Y2 = ±
and show that they
are in fact the same graph. In this problem, you will need to limit your domain
or
x
values to intervals where cosine is either negative or positive and enter the
appropriate radical for Y2.
To do this, you will turn the calculator on and press Y= . Press CL
to clear Y1 of an old expression.
Now enter the cos for Y1 by pressing cos X/
θ
/T/
n
a/b 2 ENTER and
the for Y2 (limiting to where cosine is positive) by pressing CL
2ndF a/b 1 + cos X/
θ
/T/
n
▼
2 ENTER . Cos will be
positive for a viewing window of 0 <
x
<
π
. Enter this viewing window by
pressing WINDOW 0 ENTER 2ndF
π
ENTER 2ndF
π
÷
2 ENTER
(–)
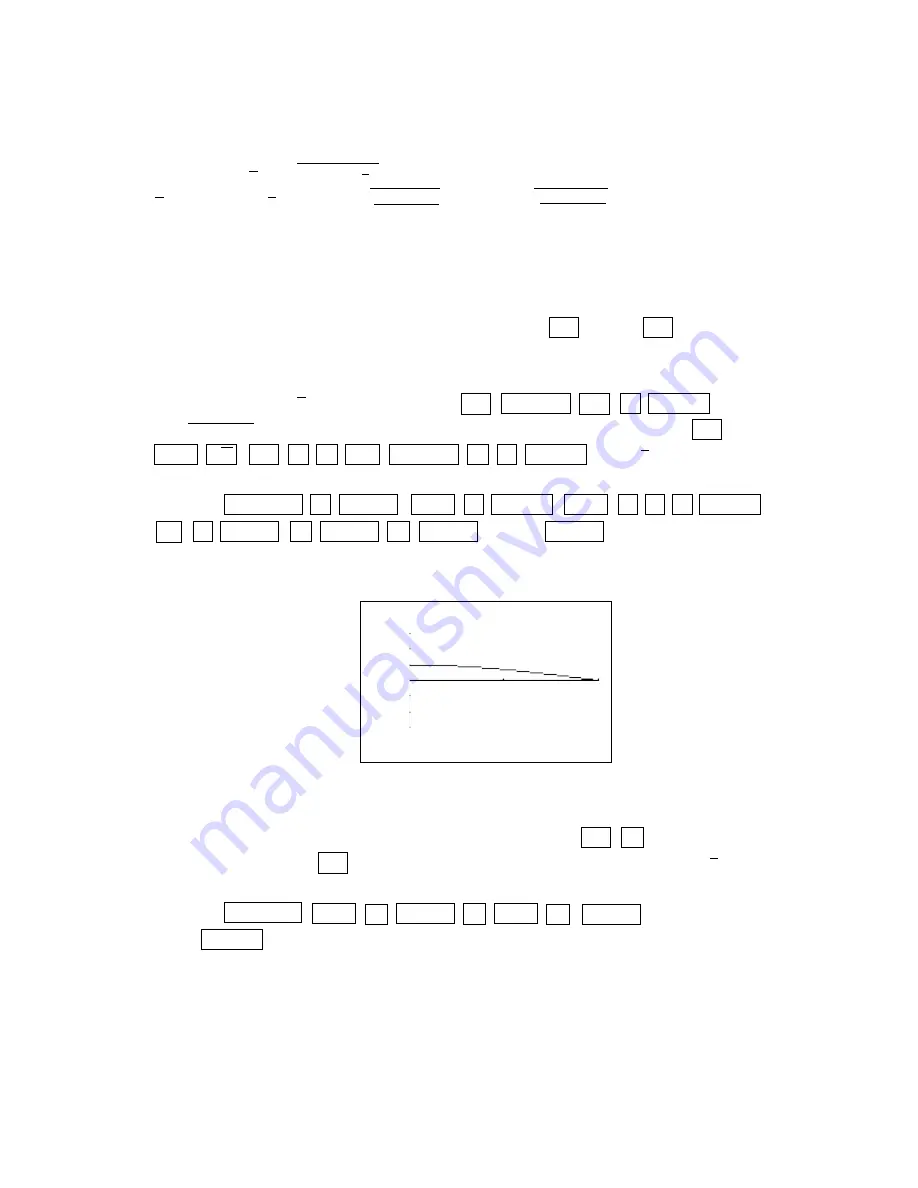
3 ENTER 3 ENTER 1 ENTER . Press GRAPH to view the graphs.
Notice they appear as one graph.
To verify the formula for where cosine is negative, press Y=
▼
to access the
Y2 prompt and press (–) to insert a negative in front of the radical. Cos will
be negative for a viewing window of
π
<
x
< 3
π
. Enter this viewing window by
pressing WINDOW 2ndF
π
ENTER 3 2ndF
π
ENTER .
Press GRAPH to view the graphs. Notice they appear as one graph.
12
Graphical Verification of Formulas and Identities/TRIGONOMETRY USING THE SHARP EL-9600
θ
2
θ
2
θ
2
1 + cos
θ
2
1 + cos
θ
2
x
2
x
2
x
2
x
2
1 + cos
x
2
√
√
√
√










































