275
APPENDIX
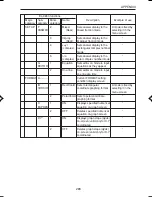
3
χ
2
(
f (
χ
2
, df) =
1
2Γ
(
)
df
2
χ
2
2
(
)
df
2
–1
e
χ
2
2
(
–
)
However:
Γ
(s) =
∫
x
s–1
e
–x
dx
∞
0
df: Degree of freedom
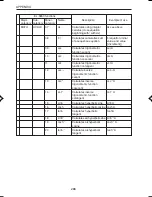
4
pdfF(
f (x) =
Γ
(
)
m+n
2
Γ
(
)
m
2
Γ
(
)
n
2
(
)
m
n
m
2
X
m
2
–1
(1+
)
mx
n
m+n
2
–
However:
Γ
(s) =
∫
x
s–1
e
–x
dx
∞
0
m: Degree of freedom of
numerator
n: Degree of freedom of
denominator
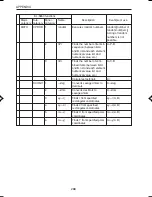
5
pdfbin(
6
pdfpoi(
n: Trial number (integers
greater than 0)
p: Success probability
(0
≤
p
≤
1)
c: Success number
P (x=0) = (1–p)
n
P (x=c+1) =
(n–c) p
(c+1)(1–p)
P (x=c)
f (x) =
e
–
µ
µ
x
x!
(x=0, 1, 2, ...)
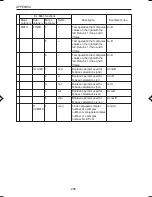
7
pdfgeo(
x: First successful trial number
f (x) = p(1 – p)
x–1
(c=0,1,…, n–1)
EL-9650-Appendix (265-281)
8/3/00, 5:06 PM
275
Summary of Contents for EL-9650
Page 10: ...viii ...
Page 46: ...36 CHAPTER 1 ...
Page 230: ...220 CHAPTER 9 ...
Page 268: ...258 CHAPTER 12 ...
Page 349: ...339 APPENDIX When coordinate system is Rect param or polar ...
Page 350: ...340 APPENDIX When coordinate system is Seq F STYLE2 E STYLE1 ...
Page 352: ...342 APPENDIX ...
Page 353: ...343 APPENDIX on Program screen ...
Page 354: ...344 APPENDIX ...
Page 355: ...345 APPENDIX ...
Page 356: ...346 APPENDIX ...
Page 357: ...347 APPENDIX ...
Page 358: ...348 APPENDIX ...