67
Matrix Calculation
In a certain year (year 0), the share of manufacturer A is 10% and the
share of manufacturer B is 90%. Manufacturer A then releases a new
product, and each following year it maintains 90% of the share a
k
it had
the previous year (year k), and usurps 20% of the share b
k
of
manufacturer B.
Find the transition matrix for this process and the shares of
manufacturers A and B after 2 years.
The share of each company after one year is expressed as follows using
a
0
and b
0
.
Thus, a
1
and b
1
are
The transition matrix is
: This is equal to matA
2
.
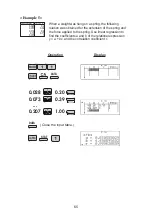
Answer
0.9 0.2
0.1 0.8
A =
0.83 0.34
0.17 0.66
A
2
=
a
1
= 0.9a
0
+ 0.2b
0
b
1
= (1-0.9)a
0
+ (1-0.2)b
0
Expressing a
2
and b
2
using a
0
and b
0
gives
a
2
= 0.9(0.9a
0
+ 0.2b
0
) + 0.2(0.1a
0
+ 0.8b
0
)
= (0.9 x 0.9 + 0.2 x 0.1)a
0
+ (0.9 x 0.2 + 0.2 x 0.8)b
0
= 0.83a
0
+ 0.34b
0
b
2
= 0.1(0.9a
0
+ 0.2b
0
) + 0.8(0.1a
0
+ 0.8b
0
)
= (0.1 x 0.9 + 0.8 x 0.1)a
0
+ (0.1 x 0.2 + 0.8 x 0.8)b
0
= 0.17a
0
+ 0.66b
0
In the same way, after two years
a
2
= 0.9a
1
+ 0.2b
1
b
2
= 0.1a
1
+ 0.8b
1
a
1
= 0.9a
0
+ 0.2b
0
b
1
= 0.1a
0
+ 0.8b
0
In summary,
a
2
= 0.83a
0
+ 0.34b
0
b
2
= 0.17a
0
+ 0.66b
0
Manufacturer A
Share 10%
20%
10%
Manufacturer B
Share 90%
<Example>
(This example is for EL-W516T only.)
Summary of Contents for EL-W516T
Page 1: ...SCIENTIFIC CALCULATOR OPERATION GUIDE SCIENTIFIC CALCULATOR OPERATION GUIDE EL W535TG W516T ...
Page 32: ...32 Example Operation Absolute Value Returns an absolute value Display 3 4 ...
Page 35: ...35 20 30 20 17 2 30 17 2 Trigonometric Functions ...
Page 37: ...37 4 8 12 16 Trigonometric Functions ...
Page 48: ...48 3 10 20 3000 x Integration calculation dx x x 100 0 dx ...