Chapter 13: Inferential Statistics and Distributions
242
Note:
L
1
â
99 and 1
â
99 specify infinity. If you want to view the area left of
upperbound
, for example,
specify
lowerbound
=
L
1
â
99.
f x
( )
1
2
πσ
--------------
e
x
μ
–
(
)
2
2
σ
2
-------------------
–
–
σ
0
>
,
=
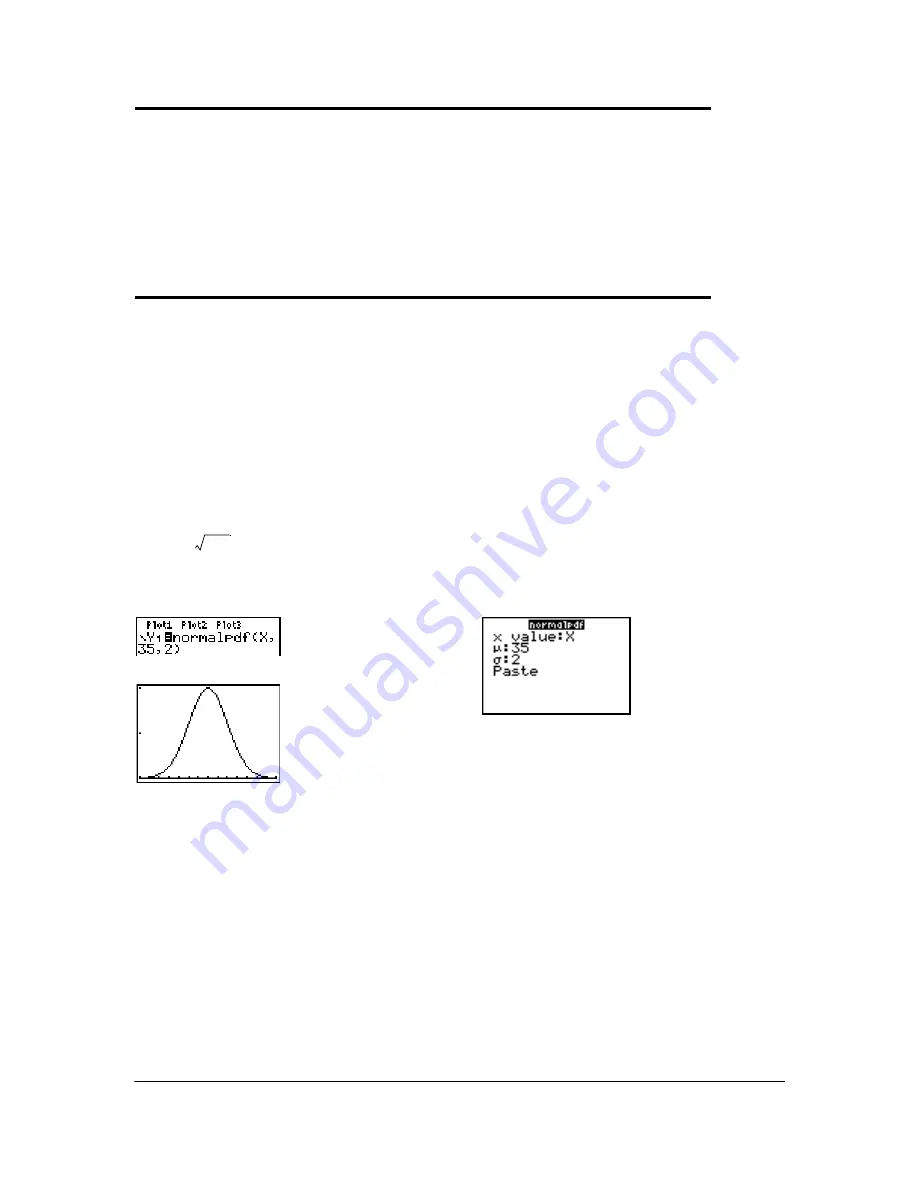
normalpdf(
normalpdf(
computes the probability density function (
) for the normal distribution at a specified
x
value. The defaults are mean
m
=0 and standard deviation
s
=1. To plot the normal distribution,
paste
normalpdf(
to the
Y= editor. The probability density function (pdf) is:
normalpdf(
x
[
,
m
,
s
]
)
Note:
For plotting the normal distribution, you can set window variables
Xmin
and
Xmax
so that the
mean
m
falls between them, and then select
0:ZoomFit
from the
ZOOM
menu.
normalcdf(
normalcdf(
computes the normal distribution probability between
lowerbound
and
upperbound
for the
specified mean
m
and standard deviation
s
. The defaults are
m
=0 and
s
=1.
A: binompdf(
Binomial probability
B: binomcdf(
Binomial cumulative density
C: poissonpdf(
Poisson probability
D: poissoncdf(
Poisson cumulative density
E: geometpdf(
Geometric probability
F: geometcdf(
Geometric cumulative density
Note:
For this example,
Xmin = 28
Xmax = 42
Xscl = 1
Ymin = 0
Ymax = .2
Yscl = .1
DISTR DRAW















































