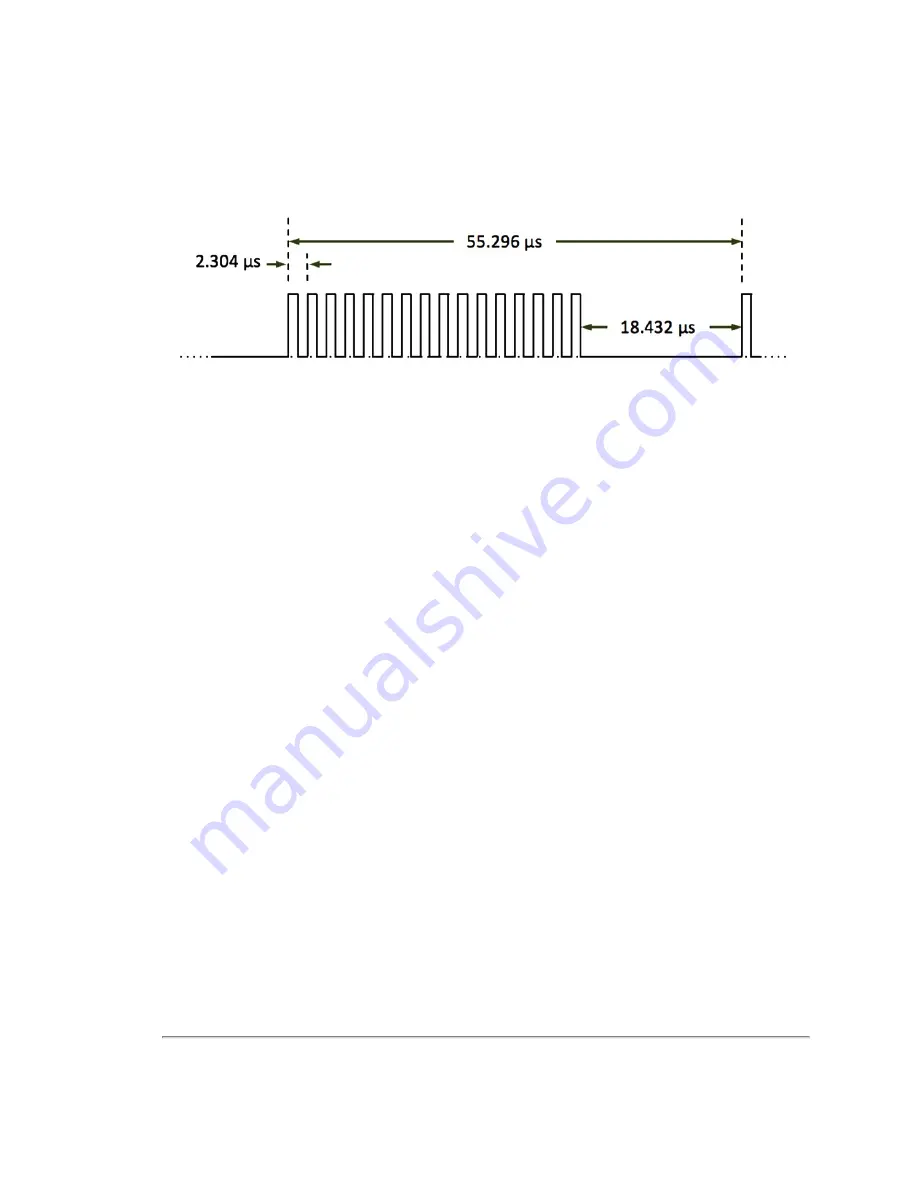
All sixteen lasers are fired and recharged every 55.296 μs. The cycle time between firings is 2.304 μs. There are 16 firings
(16 × 2.304 μs) followed by a recharge period of 18.43 μs. Therefore, the timing cycle to fire and recharge all 16 lasers is
given by (16 × 2.304 μs) + 18.43 μs = 55.296 μs.
Figure 9-7 Firing Sequence Timing
To calculate the exact time, in microseconds, of each data point, first number the points in the firing sequence as 0 to 15.
This becomes the data point index (aka Laser ID) for your calculations. Next, number the firing sequences 0 to 23. This
becomes your sequence index.
The timestamp in the packet indicates the time of the first data point in the packet. You’ll need to calculate a time offset for
each data point and then add that offset to the timestamp. See
for specific Data Point Timing Off-
for specific Data Point Timing Offsets (Dual Return Mode).
The offset equation is given by:
TimeOffset = (55.296 µs * Sequenc(2.304 µs * DataPointIndex)
To calculate the exact point time, add the TimeOffset to the timestamp.
ExactPointTime = Tim TimeOffset
Example: Calculate the timing offsets of every point in a packet, in single or dual return mode. The following is working
Python code:
def make_table(dual_mode):
timing_offsets = [[0.0 for x in range(12)] for y in range(32)] # Init matrix
# constants
full_firing_cycle = 55.296 # µs
single_firing = 2.304 # µs
# compute timing offsets
for x in range(12):
for y in range(32):
if dual_mode:
dataBlockIndex = (x - (x % 2)) + (y / 16)
else:
dataBlockIndex = (x * 2) + (y / 16)
dataPointIndex = y % 16
timing_offsets[y][x] = \
(full_firing_cycle * dataBlockIndex) + (single_firing * dataPointIndex)
return timing_offsets
To verify the values are correct, you can print them out and compare them with values in
62
VLP-16 User Manual















































