14033590.01 10/2014 GB/D
38
WIKA operating instructions model CS4S
GB
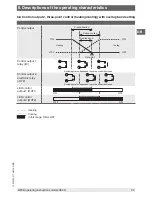
9. Control mode
9.1 PID
■
Proportional band (P)
The P component alters the manipulated variable depending on the deviation of the actual
value from the set point. The proportional band represents a “band” around the set point.
If the actual value is within the proportional band, then the variable (output) is defined in
relation to the deviation of the actual value to the set point (pulsed with relay and logic level
outputs, for current output signals it is in the range of 4 mA < MV < 20 mA). If the actual
value lies outside this band, then maximum or minimum variable is delivered (maximum
or minimum power). Enlarging the proportional band produces a more stable transient
effect, though the control is slowed down. If the proportional band is reduced, one gets
a faster control and also small disturbances are quickly controlled. If the proportional
band, however, is set too small, this can lead to undamped oscillations of the actual value
(so-called flywheel effect).
By setting the proportional band to “0” one gets an
ON
/
OFF
control mode.
Once the control variable has assumed a stable value within the range of the set point and
a constant actual value has been maintained, one gets the most suitable value by gradually
narrowing the proportional band under constant observation of the control result.
■
Integral time (I)
The I component reacts to the time-based duration of the control deviation, and removes
remaining control deviations (offset). The integral time is also referred to as the reset time,
Tn. If the integral time is reduced (I component is increased), this shortens the time taken
to reach the set point. With an integral time that is too small, this can lead to oscillations
and to unstable control results. A large integral time (smaller I component) means a lower
influence of the I term and slows down the controlling of disturbances.
■
Derivative time (D)
The D component does not react to the size and duration of the control deviation, but
rather to the rate of change of the control deviation. It works against changes in the actual
value, enables the control loop to be stable and reduces the amplitude of any overshoot or
undershoot. The derivative time is also referred to as the 'hold-back' time, Tv.
A reduction in the derivative time (D component is reduced) lowers the influence on the
variable; an increase (D component is increased) increases the influence. A derivative time
which is too large, however, can lead to oscillations.
9. Control mode