© 2001, Myricom, Inc.
-- 21 --
Revision: 27 August 2001
7. Topology Concepts
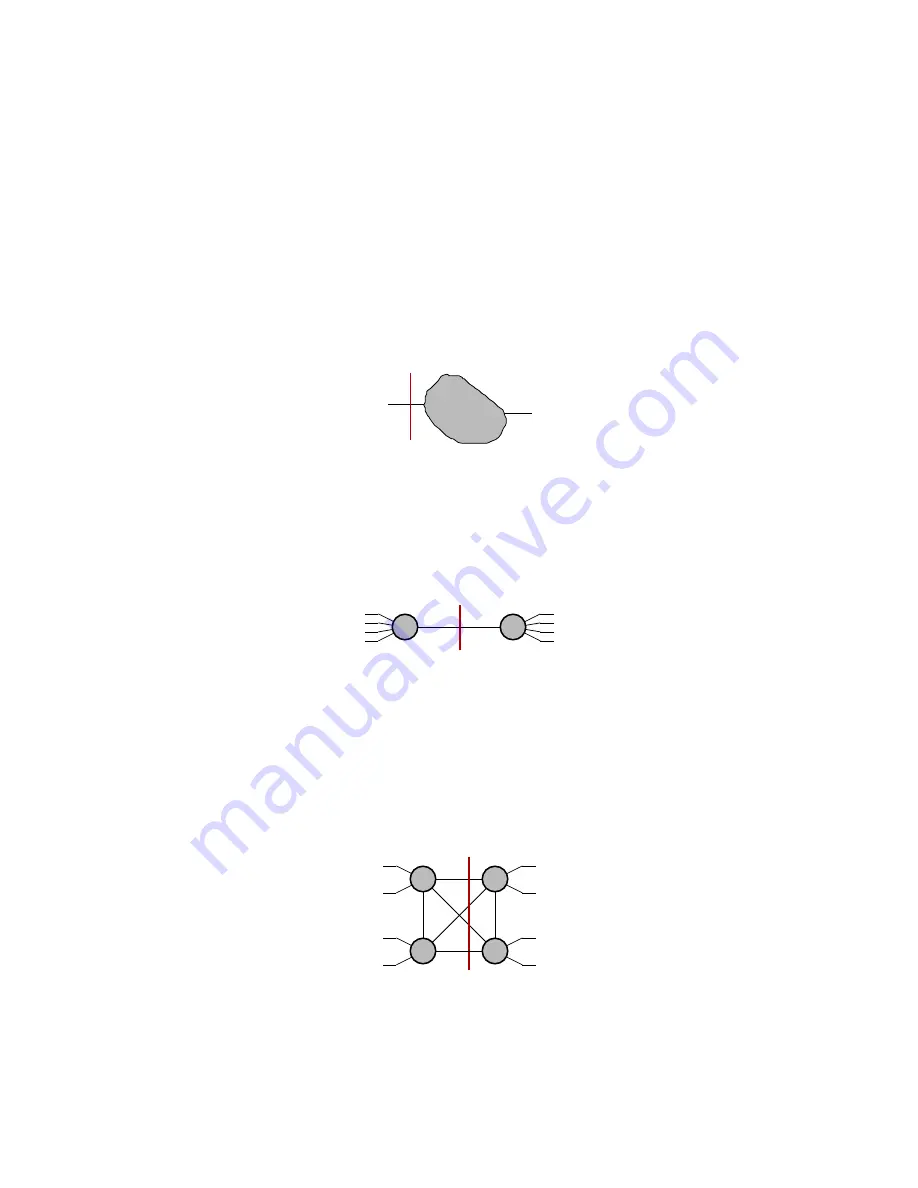
A message-passing network’s
minimum bisection,
measured in links, is defined mathematically
as the minimum number of links crossing any cut that bisects the hosts (half of the hosts on one
side of the cut, the other half on the other side). The minimum bisection provides a metric for
the minimum traffic-handling capacity of a network, no matter what the communication patterns
between the hosts may be.
The upper bound on the minimum bisection of a network of
N
hosts is
N/2
links, because, no
matter what the internal topology of the network, there will be bisecting cuts possible across half
of the host links:
Any
Topology
bisecting cut
N/2 links
N/2
hosts
N/2
hosts
A network topology that achieves this
N/2
upper bound is said to have
full
bisection.
As an example of the relevance of the minimum bisection, suppose that we wished to connect 8
hosts, and the largest (crossbar) switches available had 5 ports. One way to connect the 8 hosts
would be:
4
hosts
4
hosts
bisecting cut
1 link
The bisecting cut that exhibits the minimum bisection is evident. If the 4 hosts on the left were
sending messages to the 4 hosts on the right, and vice versa, the total traffic-handling capacity of
the network would be throttled to that of a single link. The host links would be limited to an
average of 1/4 of the link data rate, corresponding to the bisection being 1/4 full.
Here is a full-bisection network to connect the 8 hosts with 5-port switches:
2
hosts
2
hosts
bisecting cut
4 links
2
hosts
2
hosts
The bisecting cut shown is just one of many that must be considered to determine that the
minimum bisection of this topology is 4 links. For a large, unstructured network, there are so
many ways to bisect the set of hosts, and so many possible cuts for each bisection, that the
minimum bisection of the network may be difficult to compute. However, large networks will





































