So as to avoid aliasing, Odessa does not pro-
duce partials whose frequencies would exceed
the maximum frequency of 21kHz. Therefore,
the usable range of the big knob depends on
pitch frequency. For high-pitched sounds, the
frequency of most of the overtones would be
too high, hence increasing this parameter
above a certain number will not create any
audible effect.
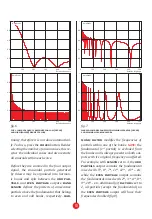
There is a fundamental problem with addi-
tive synthesis as it relates to dynamic range:
a sum of many sinusoids may be much loud-
er than just a single sinusoid (or a few). For
example, with a flat spectrum, the difference
can exceed 50dB. For practical reasons,
Odessa applies a perceptually optimized vol-
ume compensation to the output signal. You
may notice that the low-frequency partials
become quieter when the energy of higher
partials increases. The result is similar to
what you hear when comparing the loudness
of different waves from a traditional VCO.
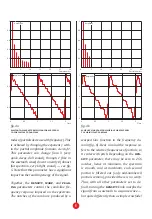
The tilt parameter determines how quickly
the spectrum decays (how quickly the ampli-
7
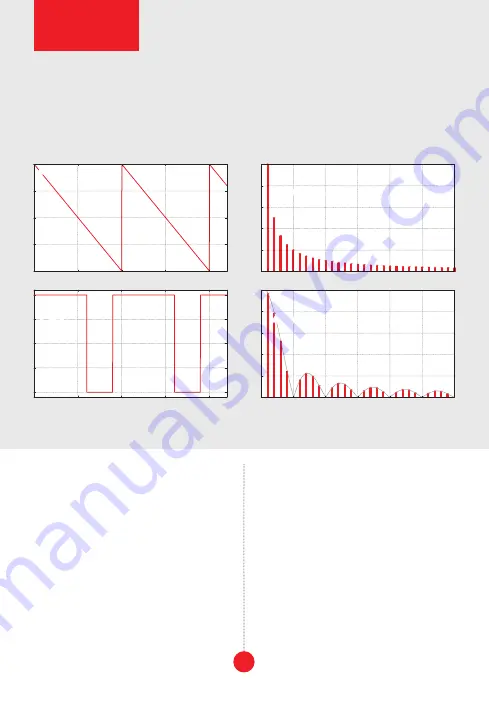
The spectrum of a saw wave contains all overtones in a naturally decaying harmonic series: the am-
plitude of each harmonic partial is inversely proportional to its number: A
n
=A
1
/n (A
1
is the amplitude
of the first, fundamental partial). Other popular waveshapes, like a pulse wave, have certain harmon-
ic partials missing because their spectra are shaped by a Sinc function which introduces a series of
notches: A
n
=A
1
×sin(2πnβ)/(2πnβ) (β is the ratio of pulse width to length of period). For a square wave,
β=0.5, which causes the Sinc function to cancel each second component so that only odd partials remain.
spectrum
parameters
0 0.5 1 1.5 2
1
0.5
0
-0.5
Time
Amplitude
0 0.5 1 1.5 2
1
0.5
0
-0.5
-1
Time
5 10 15 20 25 30
1
0.8
0.6
0.4
0.2
Partial number
0
0
5 10 15 20 25 30
1
0.8
0.6
0.4
0.2
Partial number
Amplitude
Amplitude
fig. 3
sawtooth and pulse waveforms and their respective harmonic spectra (truncated for clarity).
Amplitude