KINOVA
®
Gen3 Ultra lightweight robot
User Guide
133
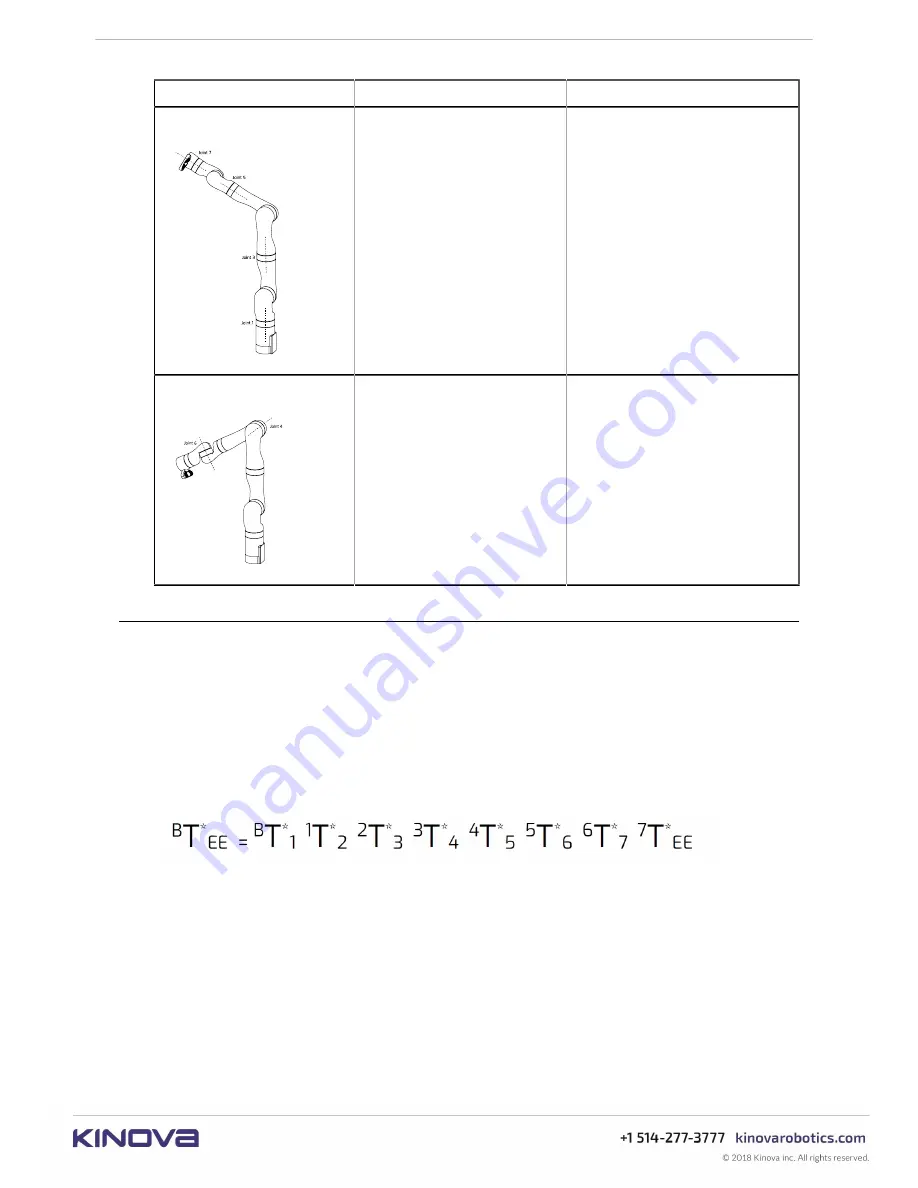
Singularity
Description
Robot behavior
Joints 2 and 6 singularity
Joint 2 is at 0° so that joints
1 and 3 are perfectly aligned
and have the same effect.
Joint 6 is at 0° so that joints
5 and 7 are perfectly aligned
and have the same effect. The
hand cannot rotate in one
direction anymore.
Due to singularity avoidance,
it’s not possible to bring joint 2
near 0° when joint 6 is near 0° in
Cartesian mode.
The control algorithms will try to
avoid the singularity by moving
joints 2 and 6 away from 0° while
moving in null space.
Joints 5 and 6 singularity
Joint 6 is at 0° so that joints
5 and 7 are perfectly aligned
and have the same effect.
Joint 5 is at 90° or at 270°
so that the axes of joint
4 and joint 6’s axis are
perpendicular. The robot
can no longer complete pure
rotations around an axis.
Due to singularity avoidance, it’s
not possible to bring joint 5 near
90° or 270° when joint 6 is near
0° in Cartesian mode.
The control algorithms will try to
avoid the singularity by moving
joint 5 away from 90° or 270°
and joint 6 away from 0° while
moving in the robot’s null space.
Reference frames and transformations
Homogeneous transforms
This section describes the homogeneous transforms for the robotic arm.
Introduction
The forward kinematics of the robotic arm are determined by homogeneous transform
matrices. These matrices represent the transformations from one frame (base, joint, or end
effector) to the next along the kinematic chain.
The overall transformation from the base frame to the end effector frame is given by:
Where:










































