Page 11-17
Using the numerical solver for linear systems
There are many ways to solve a system of linear equations with the calculator.
One possibility is through the numerical solver
‚Ï
. From the numerical
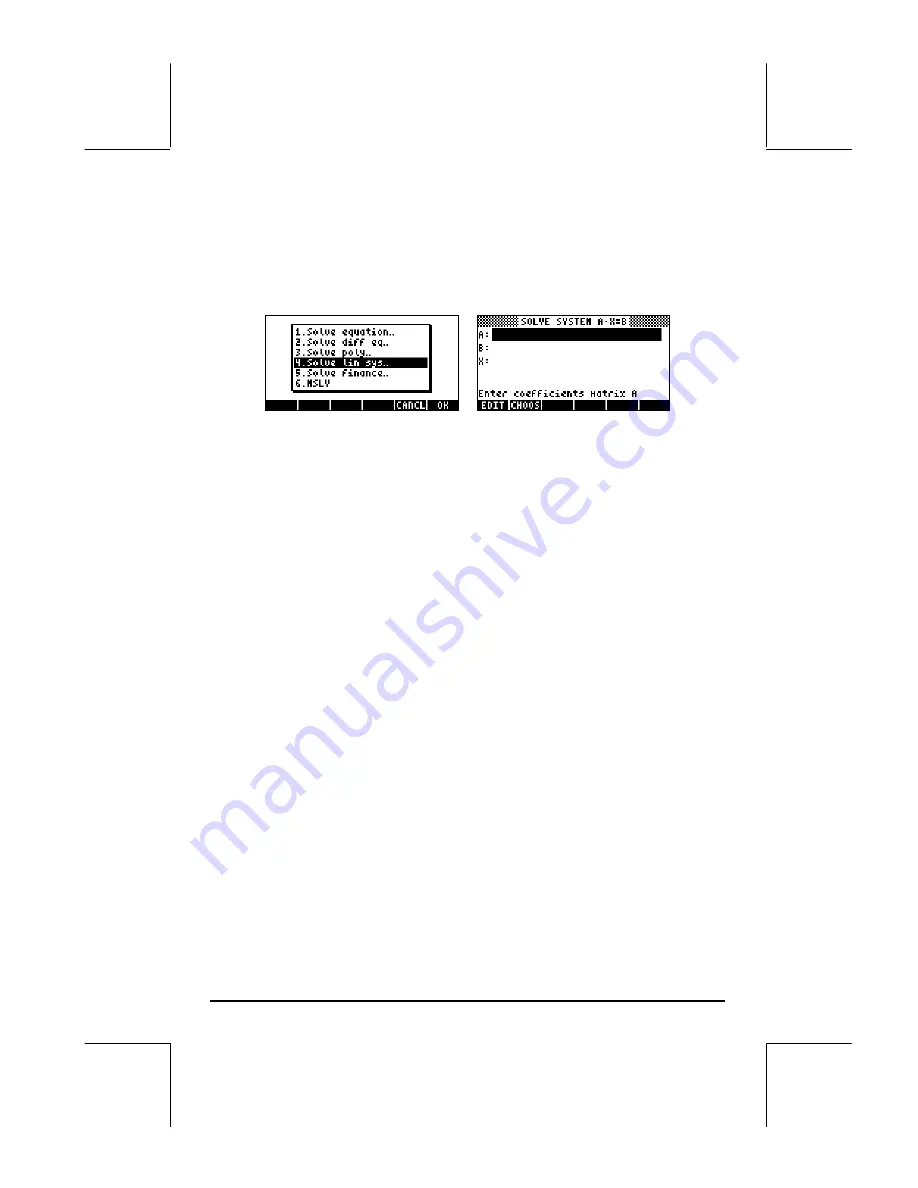
solver screen, shown below (left), select the option
4.
Solve lin sys..,
and
press
@@@OK@@@
. The following input form will be provide (right):
To solve the linear system
A
⋅
x
=
b
, enter the matrix
A
, in the format [[ a
11
,
a
12,
… ], … [….]] in the A: field. Also, enter the vector
b
in the B: field.
When the X: field is highlighted, press [SOLVE]. If a solution is available, the
solution vector
x
will be shown in the X: field. The solution is also copied to
stack level 1. Some examples follow.
A square system
The system of linear equations
2x
1
+ 3x
2
–5x
3
= 13,
x
1
– 3x
2
+ 8x
3
= -13,
2x
1
– 2x
2
+ 4x
3
= -6,
can be written as the matrix equation
A
⋅
x
=
b
, if
.
6
13
13
,
,
4
2
2
8
3
1
5
3
2
3
2
1
−
−
=
=
−
−
−
=
b
x
A
and
x
x
x
This system has the same number of equations as of unknowns, and will be
referred to as a square system. In general, there should be a unique solution
to the system. The solution will be the point of intersection of the three planes
in the coordinate system (x
1
, x
2
, x
3
) represented by the three equations.
















































